题目内容
14．已知等比数列{an}的各项均为正数，S2=7，S6=91，则S4=28．分析 由等比数列{an}的性质可得，S2，S4-S2，S6-S4成等比数列，即可得出．
解答 解：由等比数列{an}的性质可得，
S2，S4-S2，S6-S4成等比数列，
∴$（{S}_{4}-{S}_{2}）^{2}$=S2•（S6-S4），
∴$（{S}_{4}-7）^{2}$=7（91-S4），
化为${S}_{4}^{2}$-7S4-588=0，S4＞0．
解得S4=28．
故答案为：28．
点评 本题考查了等比数列的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
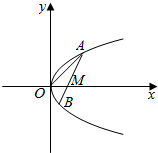如图，线段AB过x轴正半轴上一定点M（m，0），端点A、B到x轴距离之积为2m，以x轴为对称轴，过A，O，B三点作抛物线C．