题目内容
3.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\frac{\overrightarrow{a}+3\overrightarrow{b}}{5}$-$\frac{\overrightarrow{a}-\overrightarrow{b}}{2}$=$\frac{1}{5}$(3$\overrightarrow{a}$+2$\overrightarrow{b}$),求证向量$\overrightarrow{a}$和$\overrightarrow{b}$共线.分析 根据向量的混合运算和向量共线的条件即可证明.
解答 证明:$\frac{\overrightarrow{a}+3\overrightarrow{b}}{5}$-$\frac{\overrightarrow{a}-\overrightarrow{b}}{2}$=$\frac{1}{5}$(3$\overrightarrow{a}$+2$\overrightarrow{b}$),
∴2($\overrightarrow{a}$+3$\overrightarrow{b}$)-5($\overrightarrow{a}$-$\overrightarrow{b}$)=2(3$\overrightarrow{a}$+2$\overrightarrow{b}$),
∴2$\overrightarrow{a}$+6$\overrightarrow{b}$-5$\overrightarrow{a}$+5$\overrightarrow{b}$=6$\overrightarrow{a}$+4$\overrightarrow{b}$,
∴7$\overrightarrow{b}$=9$\overrightarrow{a}$,
∴$\overrightarrow{b}$=$\frac{9}{7}$$\overrightarrow{a}$,
∵非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,
∴向量$\overrightarrow{a}$和$\overrightarrow{b}$共线.
点评 本题考查向量共线的充要条件,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
18.函数f(x)=2sinx的图象( )
| A. | 关于点($\frac{π}{4}$,0)中心对称 | B. | 关于点($\frac{π}{2}$,0)中心对称 | ||
| C. | 关于点($\frac{3π}{4}$,0)中心对称 | D. | 关于点(π,0)中心对称 |
8.设集合M={x|0≤x≤2},N={y|0≤y≤2},从M到N有四种对应如图所示,其中能表示为M到N的函数关系的是( )
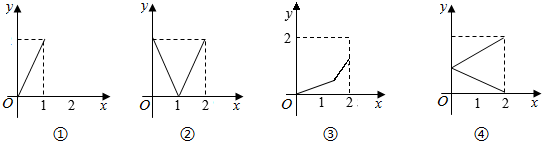

| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
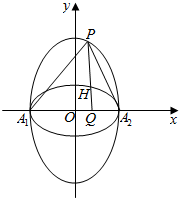 若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,A1,A2分别为椭圆C1的左右顶点,椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”
若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,A1,A2分别为椭圆C1的左右顶点,椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”