题目内容
5.设函数f(x)=4${\;}^{x-\frac{1}{2}}$+2x+1-1(1)判断函数f(x)在定义域上的单调性,并证明;
(2)若对任意t∈R,不等式f(t2-2t)>f(k-2t2)恒成立,求实数k的取值范围.
分析 (1)函数f(x)在定义域R上为单调递增.运用单调性的定义,结合指数函数的单调性;
(2)由f(x)在R上递增,即为t2-2t>k-2t2恒成立,运用参数分离和二次函数的最值的求法,即可得到k的范围.
解答 解:(1)函数f(x)在定义域R上是单调递增.
理由:f(x)=$\frac{1}{2}$(4x+4•2x)-1=$\frac{1}{2}$(2x+2)2-3,
设m<n,即有f(m)-f(n)=$\frac{1}{2}$(2m+2)2-3-$\frac{1}{2}$(2n+2)2+3
=$\frac{1}{2}$(2m-2n)(2m+2n+4),
由m<n,可得2m<2n,即2m-2n<0,则f(m)<f(n),
故f(x)在R上递增;
(2)对任意t∈R,不等式f(t2-2t)>f(k-2t2)恒成立,
由f(x)在R上递增,即为t2-2t>k-2t2恒成立,
即有k<3t2-2t的最小值,
而3t2-2t=3(t-$\frac{1}{3}$)2-$\frac{1}{3}$,当t=$\frac{1}{3}$时,取得最小值-$\frac{1}{3}$.
即有k<-$\frac{1}{3}$.
点评 本题考查函数的单调性的判断和证明,注意运用定义法,考查不等式恒成立问题的解法,注意运用单调性和参数分离,以及函数的最值的求法,属于中档题.

练习册系列答案
相关题目
16.如果已知sinα•cosα<0,sinα•tanα<0,那么角$\frac{α}{2}$的终边在( )
| A. | 第一或第二象限 | B. | 第一或第三象限 | C. | 第二或第四象限 | D. | 第四或第三象限 |
20.一次考试中,给出了9道考题,要求考生完成6道题,且前五道题中至少要完成3道,则考生选题解答的选法总数是( )
| A. | 72 | B. | 71 | C. | 73 | D. | 74 |
8.设集合M={x|0≤x≤2},N={y|0≤y≤2},从M到N有四种对应如图所示,其中能表示为M到N的函数关系的是( )
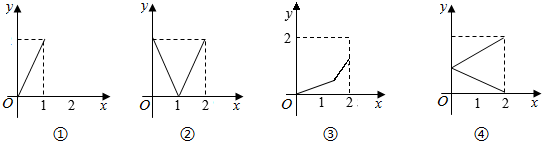

| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |