题目内容

17．已知圆C同时满足下列三个条件：①与y轴相切；②在直线y=x上截得弦长为$\sqrt{7}$；③圆心在直线x-3y=0上，求圆C的方程．

分析 设圆方程为（x-a）2+（y-b）=r2，由题意列出方程组求出a，b，由此能求出圆C的方程．

解答 解：设圆方程为（x-a）2+（y-b）=r2，
则由题意得$\left\{\begin{array}{l}{a-3b=0}\\{|a|=r}\\{（\frac{a-b}{\sqrt{2}}）^{2}+7={r}^{2}}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=3}\\{b=1}\end{array}\right.$或$\left\{\begin{array}{l}{a=-3}\\{b=-1}\end{array}\right.$，
∴圆C的方程为（x-3）2+（y-1）2=9或（x+3）2+（y+3）2=9．

点评 本题考查圆的方程的求法，是基础题，解题时要认真审题，注意圆的性质的合理运用．

练习册系列答案
相关题目
14．已知等比数列{an}的各项均为正数，S2=7，S6=91，则S4=28．
8．设集合M={x|0≤x≤2}，N={y|0≤y≤2}，从M到N有四种对应如图所示，其中能表示为M到N的函数关系的是（　　）
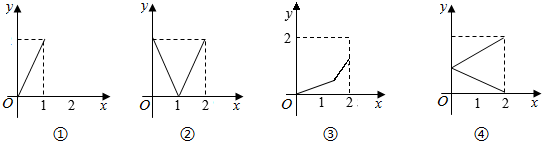
A．①②B．②③C．③④D．①④
5．平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$两两所成角相等，且|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，|$\overrightarrow{c}$|=3，则|$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$|为$\sqrt{3}$或6．
12．已知函数f（x）是定义在R上的奇函数，已知x≥0时，f（x）=x（2-x）．
（1）求函数f（x）的解析式．
（2）画出奇函数f（x）的图象．
2．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足：|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=1，|$\overrightarrow{a}$-2$\overrightarrow{b}$|≤2，则$\overrightarrow{b}$在$\overrightarrow{a}$上的投影长度的取值范围是（　　）
A．[0，$\frac{1}{13}$]B．（0，$\frac{5}{13}$]C．[$\frac{1}{13}$，1]D．[$\frac{3}{4}$，1]
9．△ABC的外接圆圆心为O，半径为2，$\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow 0$，则$\overrightarrow{CB}$在$\overrightarrow{CA}$方向上的投影为3．
6．函数$y=sin（-2x+\frac{π}{6}）$的单调递减区间是[kπ-$\frac{π}{6}$，kπ+$\frac{π}{3}$]，k∈Z．
7．设函数f（x）（x∈R）满足f（x+π）=f（x）+sinx，当0≤x＜π时，f（x）=0，则$f（\frac{7π}{6}）$=（　　）
A．$\frac{1}{2}$B．$\frac{\sqrt{3}}{2}$C．0D．-$\frac{1}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网