题目内容
19.解不等式$\frac{2x-7}{{x}^{2}+x-6}$≥1.分析 通过讨论分母的符号,得到关于x的不等式组,解出即可.
解答 解:原不等式可化为:
$\left\{\begin{array}{l}{{x}^{2}+x-6>0}\\{2x-7{≥x}^{2}+x-6}\end{array}\right.$无解,
或$\left\{\begin{array}{l}{{x}^{2}+x-6<0}\\{2x-7{≤x}^{2}+x-6}\end{array}\right.$,解得:-3<x<2,
故不等式的解集是:{x|-3<x<2}.
点评 本题考查了解不等式问题,考查分类讨论思想,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知集合A={x|(x+1)(x-2)≤0},B={x|-2<x<2},则A∩B=( )
| A. | {x|-1≤x≤2} | B. | {x|-1≤x<2} | C. | {x|-1<x<2} | D. | {x|-2<x≤1} |
4.若(2-x)2013=a0+a1x+a2x2+…+a2013x2013,则$\frac{{a}_{0}+{a}_{2}+{a}_{4}+…{+a}_{2012}}{{a}_{1}+{a}_{3}+{a}_{5}+…+{a}_{2013}}$=( )
| A. | $\frac{{3}^{2013}+1}{{3}^{2013}-1}$ | B. | -$\frac{{3}^{2013}+1}{{3}^{2013}-1}$ | ||
| C. | $\frac{{3}^{2012}+1}{{3}^{2012}-1}$ | D. | -$\frac{{3}^{2012}+1}{{3}^{2012}-1}$ |
2.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足:|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$-2$\overrightarrow{b}$|≤2,则$\overrightarrow{b}$在$\overrightarrow{a}$上的投影长度的取值范围是( )
| A. | [0,$\frac{1}{13}$] | B. | (0,$\frac{5}{13}$] | C. | [$\frac{1}{13}$,1] | D. | [$\frac{3}{4}$,1] |
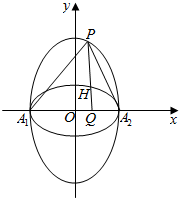 若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,A1,A2分别为椭圆C1的左右顶点,椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”
若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,A1,A2分别为椭圆C1的左右顶点,椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”