题目内容
4．已知角α终边落在点（1，3）上，则$\frac{sinα-cosα}{sinα-2cosα}$的值为2．分析 由角α终边落在点（1，3）上，利用任意角的三角函数定义求出sinα与cosα的值，代入原式计算即可求出答案．
解答 解：∵角α终边落在点（1，3）上，
∴sinα=$\frac{3}{\sqrt{10}}$，cosα=$\frac{1}{\sqrt{10}}$，
则$\frac{sinα-cosα}{sinα-2cosα}$=$\frac{\frac{3}{\sqrt{10}}-\frac{1}{\sqrt{10}}}{\frac{3}{\sqrt{10}}-2×\frac{1}{\sqrt{10}}}=2$．
故答案为：2．
点评 本题考查了同角三角函数间的基本关系，以及任意角的三角函数定义，熟练掌握基本关系是解本题的关键，是基础题．
练习册系列答案
相关题目
14．四棱锥P-ABCD的底面ABCD为平行四边形，且AB=2，BC=1，AC=2，记平面PAD与平面PBC的交线为m，平面PAB与平面PDC的交线为n，则m与n所成的锐角的余弦值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{7}{32}$ | D． | $\frac{7}{8}$ |
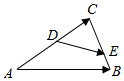如图，D，E分别是△ABC的边AC，BC上的点，且$\overrightarrow{AD}$=$\overrightarrow{DC}$，$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$．若$\overrightarrow{DE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$（λ，μ∈R），则λ+μ的值为$\frac{1}{2}$．