题目内容
设x，y为实数，且满足：（x-2014）3+2013（x-2014）=-2013，（y-2014）3+2013（y-2014）=2013，则x+y= ．
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：由题意，构造函数f（t）=t3+2013t，由f（t）的单调性，求出x-2014=2014-y，得出x+y的值．
解答：
解：根据题意，得：
∵（x-2014）3+2013（x-2014）=-[（y-2014）3+2013（y-2014）]=-2013，
∴（x-2014）3+2013（x-2014）=（2014-y）3+2013（2014-y），
令f（t）=t3+2013t，（t∈R），
∴f（t）是递增函数，且f（x-2014）=f（2014-y）；
∴x-2014=2014-y，
∴x+y=4028．
故答案为：4028．
∵（x-2014）3+2013（x-2014）=-[（y-2014）3+2013（y-2014）]=-2013，
∴（x-2014）3+2013（x-2014）=（2014-y）3+2013（2014-y），
令f（t）=t3+2013t，（t∈R），
∴f（t）是递增函数，且f（x-2014）=f（2014-y）；
∴x-2014=2014-y，
∴x+y=4028．
故答案为：4028．
点评：本题考查了函数的单调性的判定及其应用问题，解题时根据题意，构造函数，利用函数的单调性，是关键，是基础题．
练习册系列答案
相关题目
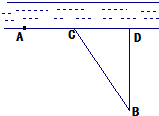甲、乙两个工厂，甲厂位于一直线河岸的岸边A处，乙厂与甲厂在河的同侧，乙厂位于离河岸40千米的B处，乙厂到河岸的垂足D与A相距50千米，两厂要在此岸边AD之间合建一个供水站C，从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元，若CD=x千米，设总的水管费用为y元，如图所示，
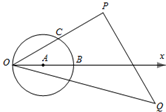如图，在极坐标系中，设极径为ρ（ρ＞0），极角为θ（0≤θ＜2π），⊙A的极坐标方程为ρ=2cosθ，点C在极轴的上方，∠AOC=圆x2+y2+ax+2=0与直线l相切于点A（-3，1）则直线l的方程为（ ）
| A、x+y+2=0 |
| B、x-2y-2=0 |
| C、x-y+4=0 |
| D、2x-y-5=0 |
已知
=a+i（a，b∈R），其中i为虚数单位，则a+b=（ ）
| 1-bi |
| 1+2i |
| A、-4 | B、4 | C、-10 | D、10 |