Question

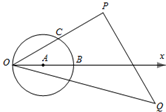如图，在极坐标系中，设极径为ρ（ρ＞0），极角为θ（0≤θ＜2π），⊙A的极坐标方程为ρ=2cosθ，点C在极轴的上方，∠AOC=

π

6

．△OPQ是以OQ为斜边的等腰直角三角形，若C为OP的中点，求点Q的极坐标．

Answer 1

考点：简单曲线的极坐标方程

专题：坐标系和参数方程

分析：由点C的极角为

π

6

，求出点C的极坐标，即得点P的极坐标；再求出点Q的极角与极径，从而得点Q的极坐标．

解答： 解：根据题意，得：
点C的极角为

π

6

，
将点C代入极坐标方程ρ=2cosθ中，
得ρ=2×

3

2

=

3

，
∴点C的极坐标为（

3

，

π

6

）；
∴点P的极坐标为（2

3

，

π

6

）；
∴点Q的极角为

π

6

-

π

4

+2π=

23π

12

，
极径为ρ=

2

×2

3

=2

6

；
∴点Q的极坐标为（2

6

，

23π

12

）．

点评：本题考查了极坐标的应用问题，解题时应结合图形，求出极坐标系中点的极角与极径，从而得极坐标，是基础题．