题目内容
已知tan(
-α)=5,则tan(
+α)= .
| π |
| 7 |
| 6π |
| 7 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:原式中的角度变形后,利用诱导公式化简,将已知等式代入计算即可求出值.
解答:
解:∵tan(
-α)=5,
∴tan(
+α)=tan[π-(
-α)]=-tan(
-α)=-5.
故答案为:-5.
| π |
| 7 |
∴tan(
| 6π |
| 7 |
| π |
| 7 |
| π |
| 7 |
故答案为:-5.
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
以下是定义域为R的四个函数,奇函数的为( )
| A、y=x3 | ||
| B、y=2x | ||
| C、y=x2+1 | ||
D、y=
|
经过双曲线x2-y2=8的右焦点且斜率为2的直线被双曲线截得的线段的长是( )
A、
| ||||
B、7
| ||||
C、2
| ||||
D、
|
命题p:幂函数y=x3在(-∞,0)上单调递减;命题q:已知函数f(x)=x3-3x2+m,若a,b,c∈[1,3],且f(a),f(b),f(c)能构成一个三角形的三边长,则4<m<8.则下列说法正确的是( )
| A、p∧q为真命题 |
| B、p∧q为假命题 |
| C、(¬p)∧q为真命题 |
| D、p∧(¬q)为真命题 |
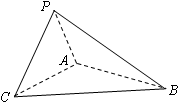 如图,平面PAC⊥平面ABC,△PAC是正三角形,∠CAB=90°,AB=2AC.
如图,平面PAC⊥平面ABC,△PAC是正三角形,∠CAB=90°,AB=2AC.