题目内容
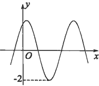 如图,函数f(x)=Asin(2x+φ)(A>0,|φ|<
如图,函数f(x)=Asin(2x+φ)(A>0,|φ|<| π |
| 2 |
| 3 |
A、(-
| ||
B、(-
| ||
C、(
| ||
D、(
|
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由函数图象可知A=2,由图象过点(0,
),可得sinφ=
,由|φ|<
,可解得φ,由2x+
=kπ,k∈Z可解得f(x)的图象的对称中心是:(
-
,0),k∈Z,对比选项即可得解.
| 3 |
| ||
| 2 |
| π |
| 2 |
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
解答:
解:由函数图象可知:A=2,由于图象过点(0,
),
可得:2sinφ=
,即sinφ=
,由于|φ|<
,
解得:φ=
,
即有:f(x)=2sin(2x+
).
由2x+
=kπ,k∈Z可解得:x=
-
,k∈Z,
故f(x)的图象的对称中心是:(
-
,0),k∈Z
当k=0时,f(x)的图象的对称中心是:(-
,0),
故选:B.
| 3 |
可得:2sinφ=
| 3 |
| ||
| 2 |
| π |
| 2 |
解得:φ=
| π |
| 3 |
即有:f(x)=2sin(2x+
| π |
| 3 |
由2x+
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
故f(x)的图象的对称中心是:(
| kπ |
| 2 |
| π |
| 6 |
当k=0时,f(x)的图象的对称中心是:(-
| π |
| 6 |
故选:B.
点评:本题主要考查由函数y=Asin(ωx+φ )的部分图象求函数的解析式,正弦函数的对称性,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
已知函数y=-x3-3x+5零点所在区间为( )
| A、(0,1) |
| B、(1,2) |
| C、(-1,0) |
| D、(2,3) |
若两个分类变量x和y的列联表为:
则x与y之间有关系的可能性为( )
| y1 | y2 | 合计 | |
| x1 | 10 | 45 | 55 |
| x2 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
| A、0.1% | B、99.9% |
| C、97.5% | D、0.25% |
平面向量
,
中,|
|≠0,
=t
(t∈R).对于使命题“?t>1,|
-
|≥|
-
|”为真的非零向量
,给出下列命题:
①?t>1,(
-
)•(
-
)≤0; ②?t>1,(
-
)•(
-
)>0;
③?t∈R,(
-
)•(
-
)<0; ④?t∈R,(
-
)•(
-
)<0.
则以上四个命题中的真命题是( )
| a |
| b |
| a |
| b |
| a |
| c |
| b |
| c |
| a |
| c |
①?t>1,(
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| a |
③?t∈R,(
| c |
| a |
| c |
| b |
| c |
| a |
| c |
| b |
则以上四个命题中的真命题是( )
| A、①④ | B、②③ |
| C、①②④ | D、①③④ |
从3名语文老师、4名数学老师和5名英语老师中选派5人组成一个支教小组,则语文、数学和英语老师都至少有1人的选派方法种数是( )
| A、590 | B、570 |
| C、360 | D、210 |
 如图,为测量坡高MN,选择A和另一个山坡的坡顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知坡高BC=50米,则坡高MN=
如图,为测量坡高MN,选择A和另一个山坡的坡顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知坡高BC=50米,则坡高MN=