题目内容
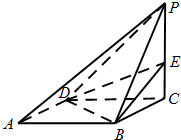 已知底面是正方形的四棱锥P-ABCD,PC⊥底面ABCD,E是侧棱PC上的动点.
已知底面是正方形的四棱锥P-ABCD,PC⊥底面ABCD,E是侧棱PC上的动点.(1)若E为PC的中点,求证:PA∥面BDE;
(2)证明:不论点E在何位置,都有BD⊥AE.
考点:直线与平面平行的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)设AC∩BD=O,可得EO∥PA,再利用直线和平面平行的判定定理证得PA∥面BDE.
(2)由PC⊥底面ABCD,可得BD⊥PC;由 底面ABCD是正方形,可得BD⊥AC,利用直线和平面垂直的判定定理可得BD⊥平面PAC,从而证得BD⊥AE.
(2)由PC⊥底面ABCD,可得BD⊥PC;由 底面ABCD是正方形,可得BD⊥AC,利用直线和平面垂直的判定定理可得BD⊥平面PAC,从而证得BD⊥AE.
解答:
(1)证明:底面是正方形的四棱锥P-ABCD,PC⊥底面ABCD,设AC∩BD=O,则O为AC的中点.
再根据E为PC的中点,可得EO∥PA.
∵PA?面BDE,EO?面BDE,∴PA∥面BDE.
(2)证明:由PC⊥底面ABCD,可得BD⊥PC;∵底面ABCD是正方形,∴BD⊥AC.
再根据 AC∩PC=C,可得BD⊥平面PAC.
而AE?平面PAC,∴BD⊥AE.
再根据E为PC的中点,可得EO∥PA.
∵PA?面BDE,EO?面BDE,∴PA∥面BDE.
(2)证明:由PC⊥底面ABCD,可得BD⊥PC;∵底面ABCD是正方形,∴BD⊥AC.
再根据 AC∩PC=C,可得BD⊥平面PAC.
而AE?平面PAC,∴BD⊥AE.
点评:本题主要考查直线和平面平行的判定定理,直线和平面垂直的判定定理的应用,属于基础题.

练习册系列答案
相关题目
 如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA上,且HA1=1.点E,F分别为棱B1C,C1C的中点,P是侧面BCC1B1内一动点,且满足PE⊥PF.则当点P运动时,|HP|2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA上,且HA1=1.点E,F分别为棱B1C,C1C的中点,P是侧面BCC1B1内一动点,且满足PE⊥PF.则当点P运动时,|HP|2的最小值是( )A、7-
| ||
B、27-6
| ||
C、51-14
| ||
D、14-2
|
利用计算机产生0~1之间的均匀随机数a,则事件“4a-1<0”发生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知P(-2,0)、Q(2,0)若点M是抛物线y2=4x上的动点,则
的最大值为( )
| |MP| |
| |MQ| |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
 在长方体ABCDA1B1C1D1中,E、F、E1、F1分别是AB、CD、A1B1、C1D1的中点.求证:平面A1EFD1∥平面BCF1E1.
在长方体ABCDA1B1C1D1中,E、F、E1、F1分别是AB、CD、A1B1、C1D1的中点.求证:平面A1EFD1∥平面BCF1E1.