题目内容
在下列结论中:
①函数y=sin(kπ-x)(k∈Z)为奇函数;
②函数y=sin4x-cos4x的最小正周期是
;
③函数y=cos(2x+
)的图象的一条对称轴为x=-
π;
④函数y=sin(
x+
)在[-2π,2π]上单调减区间是[-2π, -
]∪[
, 2π].
其中正确结论的序号为 (把所有正确结论的序号都填上).
①函数y=sin(kπ-x)(k∈Z)为奇函数;
②函数y=sin4x-cos4x的最小正周期是
| π |
| 2 |
③函数y=cos(2x+
| π |
| 3 |
| 2 |
| 3 |
④函数y=sin(
| 1 |
| 2 |
| π |
| 3 |
| 5π |
| 3 |
| 2π |
| 3 |
其中正确结论的序号为
考点:命题的真假判断与应用
专题:三角函数的图像与性质,简易逻辑
分析:①对k分类讨论可得:函数y=sin(kπ-x)=(-1)k+1sinx(k∈Z)为奇函数;
②利用倍角公式可得:函数y=sin4x-cos4x=-cos2x,其最小正周期是π;
③由于f(-
)=cos[2×(-
)+
]=cos(-π)=-1,可知函数y=cos(2x+
)的图象的一条对称轴为x=-
π;
④由
+2kπ≤
x+
≤
+2kπ,解得
+4kπ≤x≤4kπ+
(k∈Z).分别取k=-1,0即可得出函数y=sin(
x+
)在[-2π,2π]上单调减区间.
②利用倍角公式可得:函数y=sin4x-cos4x=-cos2x,其最小正周期是π;
③由于f(-
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
④由
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 3 |
| 7π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
解答:
解:①函数y=sin(kπ-x)=(-1)k+1sinx(k∈Z)为奇函数,正确;
②函数y=sin4x-cos4x=-cos2x,其最小正周期是π,因此不正确;
③∵f(-
)=cos[2×(-
)+
]=cos(-π)=-1,因此函数y=cos(2x+
)的图象的一条对称轴为x=-
π,正确;
④由
+2kπ≤
x+
≤
+2kπ,解得
+4kπ≤x≤4kπ+
(k∈Z).当k=-1时,函数f(x)的单调递减区间为[-2π,-
];当k=0时,函数f(x)的单调递减区间为[
,2π],可得函数y=sin(
x+
)在[-2π,2π]上单调减区间是[-2π,-
],[
,2π].其次其单调区间不能用“∪”,因此不正确.
其中正确结论的序号为①③.
故答案为:①③.
②函数y=sin4x-cos4x=-cos2x,其最小正周期是π,因此不正确;
③∵f(-
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
④由
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 3 |
| 7π |
| 3 |
| 5π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 5π |
| 3 |
| π |
| 3 |
其中正确结论的序号为①③.
故答案为:①③.
点评:本题考查了三角函数的图象与性质、简易逻辑的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
下列判断错误的是( )
| A、“am2<bm2”是“a<b”的充分不必要条件 |
| B、若f′(x0)=0,则x=x0是函数y=f(x)的极值点 |
| C、函数y=f(x)满足f(x+1)=f(1-x),则其图象关于直线x=1对称 |
| D、定义在R上的函数y=f(x)满足f(x+1)=-f(x),则周期为2 |
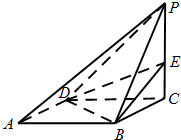 已知底面是正方形的四棱锥P-ABCD,PC⊥底面ABCD,E是侧棱PC上的动点.
已知底面是正方形的四棱锥P-ABCD,PC⊥底面ABCD,E是侧棱PC上的动点.