题目内容
若方程x2-2mx+4=0的两个不等实数根在[0,3]内,则实数m的取值范围是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:利用方程对应的二次函数的零点与判别式、对称轴及区间端点处的函数值的关系即可得出.
解答:
解:令f(x)=x2-2mx+4,
∵方程x2-2mx+4=0的两个不等实数根在[0,3]内,
∴m满足
,即:
,解得2<m<
,
∴实数m的取值范围是(2,
).
故答案为:(2,
).
∵方程x2-2mx+4=0的两个不等实数根在[0,3]内,
∴m满足
|
|
| 13 |
| 6 |
∴实数m的取值范围是(2,
| 13 |
| 6 |
故答案为:(2,
| 13 |
| 6 |
点评:熟练掌握二次函数的图象与性质是解题的关键.考查转化思想的应用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
若双曲线x2-
=1的一个焦点与抛物线y2=8x的焦点重合,则此双曲线的渐近线方程为( )
| y2 |
| m |
| A、x±y=0 | ||
B、
| ||
C、
| ||
D、
|
一个焦点为(-6,0),离心率为2的双曲线方程( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
| D、以上都不对 |
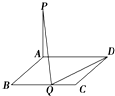 如图,在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,BC边上存在点Q,使得PQ⊥QD,则实数a的取值范围是
如图,在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,BC边上存在点Q,使得PQ⊥QD,则实数a的取值范围是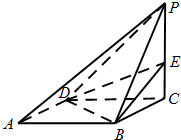 已知底面是正方形的四棱锥P-ABCD,PC⊥底面ABCD,E是侧棱PC上的动点.
已知底面是正方形的四棱锥P-ABCD,PC⊥底面ABCD,E是侧棱PC上的动点.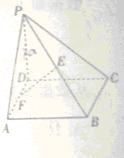 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,且PD=AB=a,E是PB的中点,F是AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,且PD=AB=a,E是PB的中点,F是AD的中点.