题目内容
函数f（x）=exlna+2x在（0，f（0））处的切线与直线3x-y-5=0平行，则a= ．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出原函数的导函数得到函数在x=0处的导数，由函数f（x）=exlna+2x在（0，f（0））处的切线与直线3x-y-5=0平行知f′（0）=3，由此列式求得a的值．
解答：
解：由f（x）=exlna+2x，得f′（x）=exlna+2，
∴f′（0）=lna+2，
∵函数f（x）=exlna+2x在（0，f（0））处的切线与直线3x-y-5=0平行，
∴lna+2=3，即lna=1，解得a=e．
故答案为：e．
∴f′（0）=lna+2，
∵函数f（x）=exlna+2x在（0，f（0））处的切线与直线3x-y-5=0平行，
∴lna+2=3，即lna=1，解得a=e．
故答案为：e．
点评：本题考查利用导数研究曲线上某点处的切线方程，函数在某点处的导数，就是曲线上过该点的切线的斜率，是中档题．
练习册系列答案
相关题目
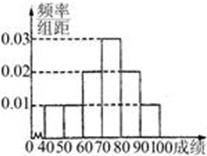我校举办安全法规知识竞赛，从参赛的高一、高二学生中各抽出100人的成绩作为样本．对高一年级的100名学生的成绩进行统计，并按[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]分组，得到成绩分布的频率分布直方图（如图）．在锐角△ABC中，∠A=2∠B，∠A、∠B的对边长分别是a、b，则
的取值范围是（ ）
| b |
| b+a |
A、（
| ||||||
B、（
| ||||||
C、（
| ||||||
D、（
|