题目内容
19.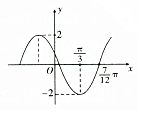 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,若f(α)=1,则cos(2α+$\frac{π}{3}$)的值是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,若f(α)=1,则cos(2α+$\frac{π}{3}$)的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
分析 由题意,可得A=2,图象过($\frac{π}{3}$,-2)和($\frac{7}{12}π$,0),可得周期T=4×$(\frac{7π}{12}-\frac{π}{3})$,从而求出ω.将坐标带入求出φ,根据f(α)=1,求出有关系α的关系式,求解出cos(2α+$\frac{π}{3}$)的值.
解答 解:由题意,可得A=2,图象过($\frac{π}{3}$,-2)和($\frac{7}{12}π$,0),可得周期T=4×$(\frac{7π}{12}-\frac{π}{3})$,即T=$\frac{2π}{ω}$=π
∴ω=2.
∴f(x)=2sin(2x+φ)
将坐标($\frac{π}{3}$,-2)带入,可得$\frac{2π}{3}$+φ=kπ$-\frac{π}{2}$,k∈Z,
∵0<φ<π,
∴φ=$\frac{5π}{6}$
可得f(x)的解析式为f(x)=2sin(2x+$\frac{5π}{6}$)
那么f(α)=2sin(2α+$\frac{5π}{6}$)=1
sin(2α+$\frac{5π}{6}$)=$\frac{1}{2}$,
sin(2α+$\frac{π}{3}$+$\frac{π}{2}$)=cos(2α$+\frac{π}{3}$)=$\frac{1}{2}$,
故选A.
点评 本题主要考查三角函数的图象和性质,根据图象求出函数的解析式是解决本题的关键.要求熟练掌握函数图象之间的变化关系.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
9.sin40°sin10°+cos40°sin80°=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | cos50° | D. | $\frac{{\sqrt{3}}}{2}$ |
7.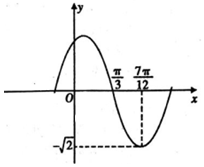 函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )
函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )
 函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )
函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,若方程f(x)=a在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上有两个不相等的实数根,则a的取值范围是( )| A. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | B. | [-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$) | C. | [-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$) | D. | [$\frac{\sqrt{6}}{2}$,$\sqrt{2}$) |
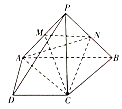 如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥
如图所示,四棱锥P-ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥CD,AD⊥CD,PC⊥