题目内容
14．以角θ的顶点为坐标原点，始边为x轴的非负半轴，建立平面直角坐标系，角θ终边过点P（1，2），则$tan（θ+\frac{π}{4}）$=-3．分析 根据题意任意角三角函数的定义即可求出tanα，进而利用两角和的正切函数公式即可计算得解．
解答 解：由题意可得 x=1，y=2，
∴tanα=$\frac{y}{x}$=2，
∴$tan（θ+\frac{π}{4}）$=$\frac{1+tanθ}{1-tanθ}$=$\frac{1+2}{1-2}$=-3．
故答案为：-3．
点评 本题考查任意角的三角函数的定义，两角和的正切函数公式的应用，利用任意角的定义是解题的关键，属于基础题．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
4．点P（x，y）的坐标满足约束条件$\left\{\begin{array}{l}x-2y≥0\\ x+2y+4≥0\\ 7x+2y-8≤0\end{array}\right.$，由点P向圆C：（x+2）2+（y-1）2=1作切线PA，切点为A，则线段|PA|的最小值为（ ）
| A． | $\frac{{4\sqrt{5}}}{5}$ | B． | $\frac{{\sqrt{55}}}{5}$ | C． | $\sqrt{19}$ | D． | $\frac{{\sqrt{33}}}{2}$ |
9．将函数f（x）=sinωx（ω＞0）的图象向左平移$\frac{π}{4ω}$个单位得到函数g（x）的图象，若函数g（x）的图象关于直线x=ω对称且在区间（-ω，ω）内单调递增，则ω的值为（ ）
| A． | $\frac{{3\sqrt{π}}}{2}$ | B． | $\frac{π}{4}$ | C． | $\frac{{\sqrt{π}}}{2}$ | D． | $\frac{3π}{2}$ |
19．
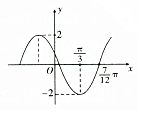已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象如图所示，若f（α）=1，则cos（2α+$\frac{π}{3}$）的值是（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象如图所示，若f（α）=1，则cos（2α+$\frac{π}{3}$）的值是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{3}$ |
