题目内容
10．若实数x，y满足$\left\{\begin{array}{l}{y≥0}\\{x-2y≥0}\\{x+y≤5}\end{array}\right.$，则x+2y的最小值是0．分析 先画出线性约束条件表示的可行域，再将目标函数赋予几何意义，即可求出z=x+2y的最小值．
解答 
解：依题意作出可行性区域，
标函数z=x+2y可看做斜率为-$\frac{1}{2}$的动直线在y轴上的纵截距．
数形结合可知，当动直线过点O时，
目标函数值最小z=0+0=0
故答案为：0．
点评 本题主要考查了线性规划的思想和方法，二元一次不等式组表示平面区域，数形结合的思想方法，属基础题．
练习册系列答案
相关题目
如图，利用随机模拟的方法可以估计图中由曲线y=$\frac{{x}^{2}}{2}$与两直线x=2及y=0所围成的阴
18．已知三棱锥S-ABC外接球的直径SC=6，且AB=BC=CA=3，则三棱锥S-ABC的体积为（ ）
| A． | $\frac{{3\sqrt{2}}}{4}$ | B． | $\frac{{9\sqrt{2}}}{4}$ | C． | $\frac{{3\sqrt{2}}}{2}$ | D． | $\frac{{9\sqrt{2}}}{2}$ |
已知圆O：x2+y2=r2，直线$x+2\sqrt{2}y+2=0$与圆O相切，且直线l：y=kx+m与椭圆C：$\frac{x^2}{2}+{y^2}=1$相交于P、Q两点，O为原点．
19．
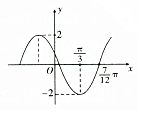已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象如图所示，若f（α）=1，则cos（2α+$\frac{π}{3}$）的值是（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象如图所示，若f（α）=1，则cos（2α+$\frac{π}{3}$）的值是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{3}$ |