题目内容
已知f(x)=sin(-2x+
)+
,x∈R.
(1)求函数f(x)的最小正周期和单调增区间.
(2)函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
| π |
| 6 |
| 3 |
| 2 |
(1)求函数f(x)的最小正周期和单调增区间.
(2)函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
考点:三角函数的周期性及其求法,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)根据f(x)=sin(-2x+
)+
,可得函数的周期,即函数 y=sin(2x-
)的减区间.令
+2kπ<2x-
<
+2kπ,求得x的范围,可得f(x)的增区间.
(2)根据y=Asin(ωx+φ)的图象变换规律,得出结论.
| π |
| 6 |
| 3 |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
(2)根据y=Asin(ωx+φ)的图象变换规律,得出结论.
解答:
解:(1)∵f(x)=sin(-2x+
)+
=-sin(2x-
)+
,
∴函数的最小正周期为
=π,函数f(x)的单调增区间即函数y=sin(2x-
)的减区间.
令
+2kπ<2x-
<
+2kπ,解得kπ+
<x<kπ+
,k∈z.
故f(x)的增区间为[kπ+
,kπ+
],k∈z.
(2)把函数y=sin2x(x∈R)的图象向左平移
个单位,可得函数y=sin2(x+
)=sin(2x+
)的图象;
再把所得图象向上平移
个单位,可得函数y=sin(2x+
)+
的图象;
再把所得图象向关于y轴对称,可得函数y=sin(-2x+
)+
的图象.
| π |
| 6 |
| 3 |
| 2 |
| π |
| 6 |
| 3 |
| 2 |
∴函数的最小正周期为
| 2π |
| 2 |
| π |
| 6 |
令
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 3 |
| 5π |
| 6 |
故f(x)的增区间为[kπ+
| π |
| 3 |
| 5π |
| 6 |
(2)把函数y=sin2x(x∈R)的图象向左平移
| π |
| 12 |
| π |
| 12 |
| π |
| 6 |
再把所得图象向上平移
| 3 |
| 2 |
| π |
| 6 |
| 3 |
| 2 |
再把所得图象向关于y轴对称,可得函数y=sin(-2x+
| π |
| 6 |
| 3 |
| 2 |
点评:本题主要考查三角函数的周期性和求法,正弦函数的单调性,y=Asin(ωx+φ)的图象变换规律,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
化简:(sinα+cosα)2=( )
| A、1+sin2α |
| B、1-sinα |
| C、1-sin2α |
| D、1+sinα |
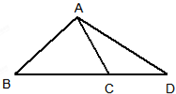 如图,在△ABC中,内角A,B,C的对边分别是a,b,c,且bsinA=acosB,D是BC延长线上的一点,AC=5,AD=7,CD=3.
如图,在△ABC中,内角A,B,C的对边分别是a,b,c,且bsinA=acosB,D是BC延长线上的一点,AC=5,AD=7,CD=3.