题目内容
10.已知函数f(x)=lnx+x与$g(x)=\frac{1}{2}a{x^2}+ax-1$(a>0)的图象有且只有一个公共点,则a所在的区间为( )| A. | $(\frac{1}{2},\frac{2}{3})$ | B. | $(\frac{2}{3},1)$ | C. | $(\frac{3}{2},2)$ | D. | $(1,\frac{3}{2})$ |
分析 设T(x)=f(x)-g(x)=lnx+x-$\frac{1}{2}a{x}^{2}$-ax+1,T′(x)=(x+1)•$\frac{1}{x}$•(1-ax),推导出T(x)在(0,$\frac{1}{a}$)上单调递增,在($\frac{1}{a}$,+∞)上单调递减,由此利用分类讨论思想能求出a所在的区间.
解答 解:设T(x)=f(x)-g(x)=lnx+x-$\frac{1}{2}a{x}^{2}$-ax+1,
在x>0时,有且仅有1个零点,
T′(x)=$\frac{1}{x}+1-ax-a$=$\frac{x+1}{x}$-a(x+1)
=(x+1)($\frac{1}{x}-a$)
=(x+1)•$\frac{1}{x}$•(1-ax),
∵a>0,x>0,∴T(x)在(0,$\frac{1}{a}$)上单调递增,在($\frac{1}{a}$,+∞)上单调递减,如右图,
当x→0时,T(x)→∞,x→+∞时,T(x)→-∞,
∴$T(\frac{1}{a})=0$,
即ln$\frac{1}{a}$+$\frac{1}{a}$-$\frac{1}{2}•\frac{1}{a}$-1+1=0,
∴ln$\frac{1}{a}$+$\frac{1}{2a}$=0,
∴lnx+$\frac{1}{2x}$在x>0上单调,
∴$ln\frac{1}{a}+\frac{1}{2a}=0$在a>0上最多有1个零点,
a=1时,$ln\frac{1}{a}$+$\frac{1}{2a}$=$\frac{1}{2}$>0,
a=2时,$ln\frac{1}{a}$+$\frac{1}{2a}$<0,
$a=\frac{3}{2}$时,$ln\frac{1}{a}+\frac{1}{2a}$<0,
∴a∈(1,$\frac{3}{2}$).
故选:D.
点评 本题考查实数值取值区间的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | {0,1} | B. | {-1,0} | C. | {-1,0,1} | D. | {0,1,2} |
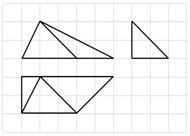
| A. | 3 | B. | 6 | C. | $2\sqrt{5}$ | D. | 5 |

| A. | -1 | B. | i-1 | C. | 0 | D. | -i |
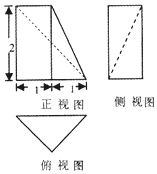
| A. | 2$\sqrt{2}$+2$\sqrt{3}$+2 | B. | 3$\sqrt{2}$+2$\sqrt{3}$+3 | C. | 2$\sqrt{2}$+$\sqrt{3}$+2 | D. | 3$\sqrt{2}$+$\sqrt{3}$+3 |
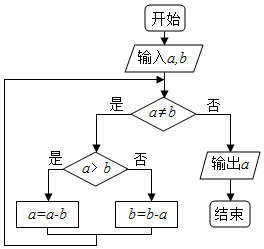 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为24,18,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为24,18,则输出的a=( )