题目内容
20．已知集合A={-2，-1，0，1，2}，B={x|（x+1）（x-2）＜0}，则A∩B=（ ）| A． | {0，1} | B． | {-1，0} | C． | {-1，0，1} | D． | {0，1，2} |
分析 根据题意，解（x+1）（x-2）＜0可得集合B，进而由集合交集的定义计算可得答案．
解答 解：根据题意，（x+1）（x-2）＜0⇒-1＜x＜2，
则B={x|（x+1）（x-2）＜0}={x|-1＜x＜2}，
又由集合A={-2，-1，0，1，2}，
则A∩B={0，1}，
故选A．
点评 本题考查集合交集的计算，关键是理解集合交集的定义．
练习册系列答案
相关题目
10．设点P是圆C：（x+4）2+（y-2）2=5上的动点，则点P到原点距离的最大值为（ ）
| A． | $\sqrt{5}$ | B． | $2\sqrt{5}$ | C． | $3\sqrt{5}$ | D． | $4\sqrt{5}$ |
8．若当$\lim_{△x→0}\frac{{f（{x_0}）-f（{x_0}+3△x）}}{2△x}$=1，则f′（x0）等于（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | -$\frac{3}{2}$ | D． | -$\frac{2}{3}$ |
15．不等式x2-|x|-2＜0（x∈R）的解集是（ ）
| A． | {x|x＜-1或x＞1} | B． | {x|x＜-2或x＞2} | C． | {x|-1＜x＜1} | D． | {x|-2＜x＜2} |
5．某算法的程序框图如图所示，若输出的y=$\frac{{\sqrt{2}}}{2}$，则输入的x的值可能为（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{2}$ | D． | $\frac{9}{2}$ |
12．
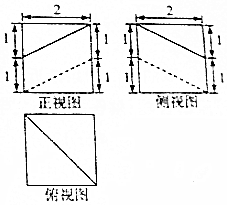某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{20}{3}$ | B． | $\frac{16}{3}$ | C． | 4 | D． | 7 |
9．已知[x]表示不超过x的最大整数．执行如右图所示的程序框图，若输入x的值为2.4，则输出z的值为（ ）
| A． | 1.2 | B． | 0.6 | C． | 0.4 | D． | -0.4 |
10．已知函数f（x）=lnx+x与$g（x）=\frac{1}{2}a{x^2}+ax-1$（a＞0）的图象有且只有一个公共点，则a所在的区间为（ ）
| A． | $（\frac{1}{2}，\frac{2}{3}）$ | B． | $（\frac{2}{3}，1）$ | C． | $（\frac{3}{2}，2）$ | D． | $（1，\frac{3}{2}）$ |