题目内容
19.某四棱锥的三视图如图所示,俯视图是一个等腰直角三角形,则该四棱锥的表面积是( )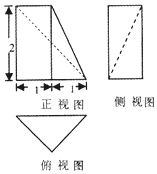
| A. | 2$\sqrt{2}$+2$\sqrt{3}$+2 | B. | 3$\sqrt{2}$+2$\sqrt{3}$+3 | C. | 2$\sqrt{2}$+$\sqrt{3}$+2 | D. | 3$\sqrt{2}$+$\sqrt{3}$+3 |
分析 由已知的四棱锥三视图,画出该四棱锥的直观图,结合图中数据求出四棱锥的表面积.
解答 解:由已知的四棱锥三视图,可得:
该四棱锥的直观图如图所示:
其底面面积为:S矩形ABCD=2×$\sqrt{2}$=2$\sqrt{2}$,
侧面S△PBC=$\frac{1}{2}$×2×1=1,
S△PCD=$\frac{1}{2}$×2×$\sqrt{2}$=$\sqrt{2}$,
S△PAB=$\frac{1}{2}$×2×2=2,
S△PAD=$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{{2}^{2}{+(\sqrt{2})}^{2}}$=$\sqrt{3}$;
∴四棱锥的表面积为
S=2$\sqrt{2}$+1+$\sqrt{2}$+2+$\sqrt{3}$=3+3$\sqrt{2}$+$\sqrt{3}$.
故选:D.
点评 本题考查了由三视图求几何体表面积的问题,判断几何体的形状及数据是解题的关键.

练习册系列答案
相关题目
9.已知[x]表示不超过x的最大整数.执行如右图所示的程序框图,若输入x的值为2.4,则输出z的值为( )

| A. | 1.2 | B. | 0.6 | C. | 0.4 | D. | -0.4 |
10.已知函数f(x)=lnx+x与$g(x)=\frac{1}{2}a{x^2}+ax-1$(a>0)的图象有且只有一个公共点,则a所在的区间为( )
| A. | $(\frac{1}{2},\frac{2}{3})$ | B. | $(\frac{2}{3},1)$ | C. | $(\frac{3}{2},2)$ | D. | $(1,\frac{3}{2})$ |
7.已知扇形的圆心角为$\frac{π}{3}$,半径为2,则扇形的弧长为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $4+\frac{2π}{3}$ |
4.执行如图所示的程序框图,输出S值为( )
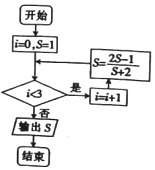

| A. | $-\frac{31}{15}$ | B. | $-\frac{7}{5}$ | C. | $-\frac{31}{17}$ | D. | $-\frac{9}{13}$ |
11.与球心距离为1的截球平面,所得的截面圆的面积为2π,则球的体积为( )
| A. | 8$\sqrt{3}$π | B. | 4$\sqrt{3}$π | C. | 4π | D. | 8π |
8.若cosθ<0,且sin2θ<0,则角θ的终边所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图所示函数图象,
如图所示函数图象,