题目内容
2．等差数列{an}的前n项和为Sn，且a1=1，a4=7，则S10=100．分析 由等差数列的通项公式求得公差d=2，然后根据等差数列的前n项和的求法解答．
解答 解：设等差数列{an}的公差为d，
由a1=1，a4=7得到：7=1+3d，
解得d=2．
所以S10=10×1+$\frac{10×9}{2}$×2=100．
故答案是：100．
点评 本题考查了等差数列的前n项和，属于基础题，熟记公式即可解答．
练习册系列答案
相关题目
12．
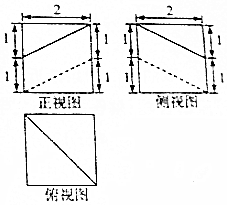某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{20}{3}$ | B． | $\frac{16}{3}$ | C． | 4 | D． | 7 |
13．已知一个几何体的三视图如图所示，则该几何体的体积为（ ）
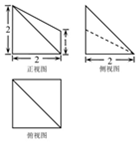
| A． | $\frac{10}{3}$ | B． | 4 | C． | $\frac{13}{3}$ | D． | 5 |
10．已知函数f（x）=lnx+x与$g（x）=\frac{1}{2}a{x^2}+ax-1$（a＞0）的图象有且只有一个公共点，则a所在的区间为（ ）
| A． | $（\frac{1}{2}，\frac{2}{3}）$ | B． | $（\frac{2}{3}，1）$ | C． | $（\frac{3}{2}，2）$ | D． | $（1，\frac{3}{2}）$ |
17．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（ ）
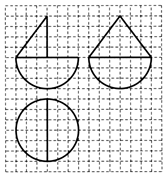
| A． | 24π | B． | 30π | C． | 42π | D． | 60π |
7．已知扇形的圆心角为$\frac{π}{3}$，半径为2，则扇形的弧长为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{6}$ | D． | $4+\frac{2π}{3}$ |
如图所示函数图象，
11．与球心距离为1的截球平面，所得的截面圆的面积为2π，则球的体积为（ ）
| A． | 8$\sqrt{3}$π | B． | 4$\sqrt{3}$π | C． | 4π | D． | 8π |
12．已知数列{an}满足an+1=$\left\{\begin{array}{l}{2{a}_{n}（0≤{a}_{n}＜\frac{1}{2}）}\\{2{a}_{n}-1（\frac{1}{2}≤{a}_{n}＜1）}\end{array}\right.$，若a1=$\frac{6}{7}$，则a2011的值为（ ）
| A． | $\frac{6}{7}$ | B． | $\frac{5}{7}$ | C． | $\frac{3}{7}$ | D． | $\frac{1}{7}$ |