题目内容
18．
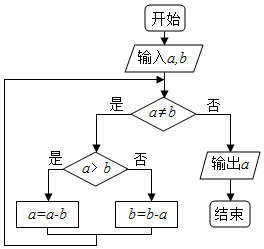如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入的a，b分别为24，18，则输出的a=（ ）| A． | 3 | B． | 4 | C． | 6 | D． | 12 |
分析 由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量a的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．
解答 解：由程序框图可知：
当a=24，b=18时，满足a＞b，则a变为24-18=6，
由b＞a，则b变为18-6=12，
由b＞a，则b变为12-6=6，
由a=b=6，
则输出的a=6．
故选：C．
点评 本题考查算法和程序框图，主要考查循环结构的理解和运用，以及赋值语句的运用，属于基础题．
练习册系列答案
相关题目
8．若当$\lim_{△x→0}\frac{{f（{x_0}）-f（{x_0}+3△x）}}{2△x}$=1，则f′（x0）等于（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | -$\frac{3}{2}$ | D． | -$\frac{2}{3}$ |
9．已知[x]表示不超过x的最大整数．执行如右图所示的程序框图，若输入x的值为2.4，则输出z的值为（ ）
| A． | 1.2 | B． | 0.6 | C． | 0.4 | D． | -0.4 |
6．已知f（x）满足f′（2）=3，则$\underset{lim}{{x}_{0}→0}$$\frac{f（2+{2x}_{0}）-f（2）}{{x}_{0}}$=（ ）
| A． | 3 | B． | 2 | C． | $\frac{3}{2}$ | D． | 6 |
13．已知一个几何体的三视图如图所示，则该几何体的体积为（ ）
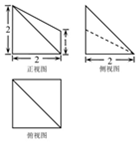
| A． | $\frac{10}{3}$ | B． | 4 | C． | $\frac{13}{3}$ | D． | 5 |
3．
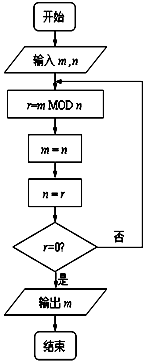如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“mMOD n”表示m除以n的余数），若输入的m，n分别为72，15，则输出的m=（ ）
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“mMOD n”表示m除以n的余数），若输入的m，n分别为72，15，则输出的m=（ ）| A． | 12 | B． | 3 | C． | 15 | D． | 45 |
10．已知函数f（x）=lnx+x与$g（x）=\frac{1}{2}a{x^2}+ax-1$（a＞0）的图象有且只有一个公共点，则a所在的区间为（ ）
| A． | $（\frac{1}{2}，\frac{2}{3}）$ | B． | $（\frac{2}{3}，1）$ | C． | $（\frac{3}{2}，2）$ | D． | $（1，\frac{3}{2}）$ |
7．已知扇形的圆心角为$\frac{π}{3}$，半径为2，则扇形的弧长为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{6}$ | D． | $4+\frac{2π}{3}$ |
8．若cosθ＜0，且sin2θ＜0，则角θ的终边所在的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |