题目内容
5.下列方格纸中每个正方形的边长为1,粗线部分是一个几何体的三视图,则该几何体最长棱的棱长是( )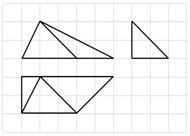
| A. | 3 | B. | 6 | C. | $2\sqrt{5}$ | D. | 5 |
分析 画出立体图,由图知,该几何体最长棱的棱长.
解答  解:画出立体图(如图).由图知,该几何体最长棱的棱长是AD=5
解:画出立体图(如图).由图知,该几何体最长棱的棱长是AD=5
故选:D.
点评 本题考查三视图,考查数形结合的数学思想,确定直观图的形状是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.不等式x2-|x|-2<0(x∈R)的解集是( )
| A. | {x|x<-1或x>1} | B. | {x|x<-2或x>2} | C. | {x|-1<x<1} | D. | {x|-2<x<2} |
13.已知一个几何体的三视图如图所示,则该几何体的体积为( )
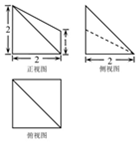

| A. | $\frac{10}{3}$ | B. | 4 | C. | $\frac{13}{3}$ | D. | 5 |
10.已知函数f(x)=lnx+x与$g(x)=\frac{1}{2}a{x^2}+ax-1$(a>0)的图象有且只有一个公共点,则a所在的区间为( )
| A. | $(\frac{1}{2},\frac{2}{3})$ | B. | $(\frac{2}{3},1)$ | C. | $(\frac{3}{2},2)$ | D. | $(1,\frac{3}{2})$ |
17.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )
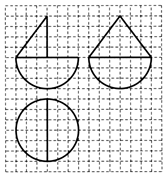

| A. | 24π | B. | 30π | C. | 42π | D. | 60π |
15.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | 8 |
 如图所示函数图象,
如图所示函数图象,