题目内容
1．在长为10cm的线段AB上任取一点P，并以线段AP为边作正方形，这个正方形的面积介于25cm2与49cm2之间的概率为$\frac{1}{5}$．分析 我们要求出以线段AP为边作正方形，这个正方形的面积介于25 cm2与4 9cm2之间对应线段AP的长，然后代入几何概型公式即可求解．
解答 解：∵以线段AP为边的正方形的面积介于25 cm2与49 cm2之间
∴线段AP的长介于5 cm与7cm之间
满足条件的P点对应的线段长2cm
而线段AB总长为10 cm
故正方形的面积介于25 cm2与49 cm2之间的概率P=$\frac{2}{10}$=$\frac{1}{5}$，
故答案为：$\frac{1}{5}$．
点评 本题考查的知识点是几何概型，几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．
练习册系列答案
相关题目
12．
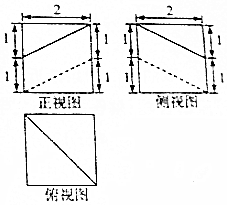某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{20}{3}$ | B． | $\frac{16}{3}$ | C． | 4 | D． | 7 |
9．已知[x]表示不超过x的最大整数．执行如右图所示的程序框图，若输入x的值为2.4，则输出z的值为（ ）
| A． | 1.2 | B． | 0.6 | C． | 0.4 | D． | -0.4 |
6．已知f（x）满足f′（2）=3，则$\underset{lim}{{x}_{0}→0}$$\frac{f（2+{2x}_{0}）-f（2）}{{x}_{0}}$=（ ）
| A． | 3 | B． | 2 | C． | $\frac{3}{2}$ | D． | 6 |
13．已知一个几何体的三视图如图所示，则该几何体的体积为（ ）
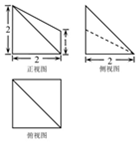
| A． | $\frac{10}{3}$ | B． | 4 | C． | $\frac{13}{3}$ | D． | 5 |
10．已知函数f（x）=lnx+x与$g（x）=\frac{1}{2}a{x^2}+ax-1$（a＞0）的图象有且只有一个公共点，则a所在的区间为（ ）
| A． | $（\frac{1}{2}，\frac{2}{3}）$ | B． | $（\frac{2}{3}，1）$ | C． | $（\frac{3}{2}，2）$ | D． | $（1，\frac{3}{2}）$ |
11．与球心距离为1的截球平面，所得的截面圆的面积为2π，则球的体积为（ ）
| A． | 8$\sqrt{3}$π | B． | 4$\sqrt{3}$π | C． | 4π | D． | 8π |