题目内容
16.已知x是1,2,2,3,x,6,7,7,8这9个数的中位数,当x2-$\frac{1}{x}$-$\frac{5}{6}$取得最大值时,1,2,2,3,x,6,7,8这9个数的平均数为$\frac{14}{3}$.分析 由已知得到x的范围以及由函数取最大值得到x值,然后求平均数.
解答 解:由x是1,2,2,3,x,6,7,7,8这9个数的中位数,得到3≤x≤6,又x2-$\frac{1}{x}$-$\frac{5}{6}$取得最大值时x=6,
所以1,2,2,3,6,6,7,7,8这9个数平均数为$\frac{1+2+2+3+6+6+7+7+8}{9}=\frac{14}{3}$;
故答案为:$\frac{14}{3}$.
点评 本题考查了样本数据的中位数以及平均数的求法;关键是明确x 的求值.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
11.若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,($\overrightarrow{a}$+$\overrightarrow{b}$)$•\overrightarrow{b}$=6,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
2.设a=tan$\frac{π}{7}$,b=$\frac{π}{7}$,c=sin$\frac{π}{7}$,则a,b,c的大小关系是( )
| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
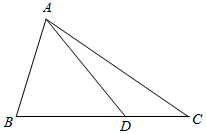 如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.
如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.