题目内容
2.设a=tan$\frac{π}{7}$,b=$\frac{π}{7}$,c=sin$\frac{π}{7}$,则a,b,c的大小关系是( )| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
分析 直接利用三角函数线,写出结果即可.
解答  解:如图:a=tan$\frac{π}{7}$,b=$\frac{π}{7}$,c=sin$\frac{π}{7}$,a=MP,b=$\widehat{AP}$,c=AT,
解:如图:a=tan$\frac{π}{7}$,b=$\frac{π}{7}$,c=sin$\frac{π}{7}$,a=MP,b=$\widehat{AP}$,c=AT,
因为S△OAT>S扇形OAP>S△OAP,
可得a>b>c.
故选:D.
点评 本题考查三角函数线的应用,考查转化思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若数列{an}满足:存在正整数T,对于任意正整数n都有an+T=an成立,则称数列{an}为周期数列,周期为T.已知数列{an}满足a1=m(m>0),${a}_{n+1}=\left\{\begin{array}{l}{{a}_{n}-1,{a}_{n}>1}\\{\frac{1}{{a}_{n}},0<{a}_{n}≤1}\end{array}\right.$,若a3=4,则m的所有可能取值为( )
| A. | {6,$\frac{5}{4}$} | B. | {6,$\frac{5}{4}$,$\frac{2}{5}$} | C. | {6,$\frac{5}{4}$,$\frac{1}{5}$} | D. | {6,$\frac{1}{5}$} |
13.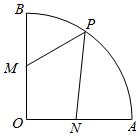 如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )
如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )
 如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )
如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )| A. | 0 | B. | 1 | C. | $\frac{3}{2}$ | D. | 1-$\frac{\sqrt{5}}{2}$ |
11.已知复数z的共轭复数$\overline{z}$,且$\overline{z}=\frac{z}{1+i}$+2(i为虚数单位),则z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
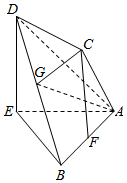 如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC、BD,G为BD的中点,AB=AC=AE=BE=2.
如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC、BD,G为BD的中点,AB=AC=AE=BE=2.