题目内容
2.设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足$\frac{{b}_{1}}{{a}_{1}}+\frac{{b}_{2}}{{a}_{2}}+…+\frac{{b}_{n}}{{a}_{n}}$=1-$\frac{1}{{2}^{n}}$,n∈N*,求{bn}的前n项和Tn.
(Ⅲ)求证:$\frac{1}{2}$≤Tn<3.
分析 (Ⅰ)设等差数列{an}的首项为a1,公差为d,由S4=4S2,a2n=2an+1,得到关于a1,d的方程组,解得即可;
(Ⅱ)先求出数列bn=$\frac{2n-1}{{2}^{n}}$,n∈N*,再由错位相减法即可求出{bn}的前n项和Tn;
(Ⅲ)根据数列的函数特征,得到Tn=3-$\frac{2n+3}{{2}^{n}}$为递增数列,根据极限思想即可证明.
解答 解:(Ⅰ)设等差数列{an}的首项为a1,公差为d,由S4=4S2,a2n=2an+1.
可得4a1+$\frac{4(4-1)d}{2}$=4(a1+a1+d),①a1+(2n-1)d=2a1+2(n-1)d+1,②
由①②解得a1=1,d=2,
∴an=1+2(n-1)=2n-1,
(Ⅱ)由已知$\frac{{b}_{1}}{{a}_{1}}+\frac{{b}_{2}}{{a}_{2}}+…+\frac{{b}_{n}}{{a}_{n}}$=1-$\frac{1}{{2}^{n}}$,n∈N*,得
当n=1时,$\frac{{b}_{1}}{{a}_{1}}$=$\frac{1}{2}$,
当n≥2时,$\frac{{b}_{n}}{{a}_{n}}$=(1-$\frac{1}{{2}^{n}}$)-(1-$\frac{1}{{2}^{n-1}}$)=$\frac{1}{{2}^{n}}$,显然n=1时符合,
∴$\frac{{b}_{n}}{{a}_{n}}$=$\frac{1}{{2}^{n}}$,n∈N*,
由(Ⅰ)知,an=2n-1,n∈N*,
∴bn=$\frac{2n-1}{{2}^{n}}$,n∈N*,
又Tn=$\frac{1}{2}$+$\frac{3}{{2}^{2}}$+$\frac{5}{{2}^{3}}$+…+$\frac{2n-1}{{2}^{n}}$,
∴$\frac{1}{2}$Tn=$\frac{1}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+$\frac{2n-3}{{2}^{n}}$+$\frac{2n-1}{{2}^{n+1}}$,
两式相减得$\frac{1}{2}$Tn=$\frac{1}{2}$+2($\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$)-$\frac{2n-1}{{2}^{n+1}}$=$\frac{3}{2}$-$\frac{1}{{2}^{n-1}}$-$\frac{2n-1}{{2}^{n+1}}$,
∴Tn=3-$\frac{2n+3}{{2}^{n}}$
(3)由(2)可知Tn=3-$\frac{2n+3}{{2}^{n}}$,
设f(x)=3-$\frac{2x+3}{{2}^{x}}$,
∴f′(x)=$\frac{2xln2+ln2-2}{{2}^{x}}$>0在(0,+∞)恒成立,
∴f(x)在(0,+∞)为增函数,
∵$\underset{lim}{n→∞}$(3-$\frac{2n+3}{{2}^{n}}$)=3,当n=1时,T1=3-$\frac{2+3}{2}$=$\frac{1}{2}$
∴$\frac{1}{2}$≤Tn<3.
点评 本题考查了等差等比数列的通项公式和前n项和公式,以及错位相减法,数列的函数特征,属于中档题.

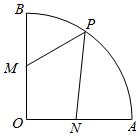 如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )
如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )| A. | 0 | B. | 1 | C. | $\frac{3}{2}$ | D. | 1-$\frac{\sqrt{5}}{2}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分条件又不必要条件 |
| A. | $\frac{2}{π}$ | B. | $\frac{1}{π}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
| A. | {1,3,5,7} | B. | {1,3,5} | C. | {3,5} | D. | {1,3} |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 满足
满足 (
( 为虚数单位),则
为虚数单位),则 的模为 .
的模为 .