题目内容
7.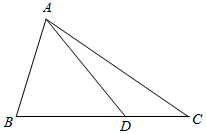 如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.
如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.(1)若∠ADC=$\frac{3}{4}$π,求AD的长;
(2)若BD=2DC,△ACD的面积为$\frac{4}{3}$$\sqrt{2}$,求$\frac{sin∠BAD}{sin∠CAD}$的值.
分析 (1)△ABD中,由正弦定理可得AD的长;
(2)利用BD=2DC,△ACD的面积为$\frac{4}{3}$$\sqrt{2}$,求出BD,DC,利用余弦定理求出AC,利用正弦定理可得结论.
解答 解:(1)∵△ABC中,cosB=$\frac{1}{3}$,∴sinB=$\frac{2\sqrt{2}}{3}$.
∵∠ADC=$\frac{3}{4}$π,∴∠ADB=$\frac{π}{4}$.
△ABD中,由正弦定理可得$\frac{AD}{\frac{2\sqrt{2}}{3}}=\frac{2}{\frac{\sqrt{2}}{2}}$,∴AD=$\frac{8}{3}$;
(2)设DC=a,则BD=2a,
∵BD=2DC,△ACD的面积为$\frac{4}{3}$$\sqrt{2}$,
∴4$\sqrt{2}$=$\frac{1}{2}×2×3a×\frac{2\sqrt{2}}{3}$,
∴a=2
∴AC=$\sqrt{4+36-2×2×6×\frac{1}{3}}$=4$\sqrt{2}$,
由正弦定理可得$\frac{4}{sin∠BAD}=\frac{2}{sin∠ADB}$,∴sin∠BAD=2sin∠ADB.
$\frac{2}{sin∠CAD}$=$\frac{4\sqrt{2}}{sin∠ADC}$,∴sin∠CAD=$\frac{\sqrt{2}}{4}$sin∠ADC,
∵sin∠ADB=sin∠ADC,
∴$\frac{sin∠BAD}{sin∠CAD}$=4$\sqrt{2}$.
点评 本题考查正弦、余弦定理的运用,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.不等式y≥2x-3表示的平面区域是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
13.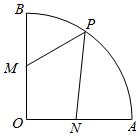 如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )
如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )
 如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )
如图,扇形AOB中,OA=1,∠AOB=90°,M是OB中点,P是弧AB上的动点,N是线段OA上的动点,则$\overrightarrow{PM}$$•\overrightarrow{PN}$的最小值为( )| A. | 0 | B. | 1 | C. | $\frac{3}{2}$ | D. | 1-$\frac{\sqrt{5}}{2}$ |
14.方程C${\;}_{16}^{{x}^{2}-x}$=C${\;}_{16}^{5x-5}$的解集是( )
| A. | {1,3,5,7} | B. | {1,3,5} | C. | {3,5} | D. | {1,3} |
