题目内容
4.已知x=1,x=3是函数f(x)=sin(ωx+φ)(ω>0)两个相邻的两个极值点,且f(x)在x=$\frac{3}{2}$处的导数f′($\frac{3}{2}$)<0,则f($\frac{1}{3}$)=$\frac{1}{2}$.分析 f(x)的周期为2×(3-1)=4,解出ω,由f′($\frac{3}{2}$)<0得出f(1)=fmax(x)=1,利用正弦函数的性质解出φ,得到f(x)的解析式,再计算f($\frac{1}{3}$).
解答 解:∵x=1,x=3是函数f(x)=sin(ωx+φ)(ω>0)两个相邻的两个极值点,
∴f(x)的周期T=$\frac{2π}{ω}$=2×(3-1)=4,∴ω=$\frac{π}{2}$.
∵f′($\frac{3}{2}$)<0,
∴f(x)在[1,3]上是减函数,∴f(1)=sin($\frac{π}{2}$+φ)=1,
∴$\frac{π}{2}$+φ=$\frac{π}{2}+2kπ$,∴φ=2kπ.
∴f($\frac{1}{3}$)=sin($\frac{π}{6}+2kπ$)=sin$\frac{π}{6}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了正弦函数的图象与性质,导数与函数单调性的关系,属于中档题.

练习册系列答案
相关题目
19.不等式y≥2x-3表示的平面区域是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
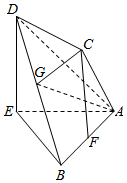 如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC、BD,G为BD的中点,AB=AC=AE=BE=2.
如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC、BD,G为BD的中点,AB=AC=AE=BE=2.