题目内容
已知点M是⊙B:(x+2)2+y2=12上的动点,点A(2,0),线段AM的中垂线交直线MB于点P.
(1)求点P的轨迹C的方程;
(2)若直线l:y=kx+m(k≠0)与曲线C交于R,S两点,D(0,-1),且有|
|=|
|,求m的取值范围.
(1)求点P的轨迹C的方程;
(2)若直线l:y=kx+m(k≠0)与曲线C交于R,S两点,D(0,-1),且有|
| RD |
| SD |
考点:直线与圆相交的性质,轨迹方程
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(1)首先根据点的图象中的位置关系确定点的轨迹是双曲线,进一步求出方程.
(2)根据(1)的结论,进一步建立直线和曲线的方程,利用|
|=|
|,进一步建立等量关系,利用直线的垂直求出参数的范围.
(2)根据(1)的结论,进一步建立直线和曲线的方程,利用|
| RD |
| SD |
解答:
(1)解:已知点M是⊙B:(x+2)2+y2=12上的动点,点A(2,0),线段AM的中垂线交直线MB于点P,
则:|PB|-|PA|=2
所以:点p的轨迹是以B、A为焦点的双曲线的左支.
由于|AB|=4
即:c=2
|PB|-|PA|=2
=2a
解得:a=
所以双曲线的方程为:
-y2=1(x<0)
(2)若直线l:y=kx+m(k≠0)与曲线C交于R,S两点
则:
整理得:(1-3k2)x2-6kmx-3m2-3=0(1-3k2≠0)
由于△>0
解得:m2+1>3k2①
设R(x1,y1),S(x2,y2)RS的中点坐标为M(x0,y0)
所以x1+x2=
,x1x2=
x0=
=
,y0=kx0+m=
M(
,
)
所以:kMD=
|
|=|
|
kMD•kRS=-1
所以:k•
=-1
解得:4m+1=3k2代入①得:m2+1>4m+1
解得:m>4或m<0
由于3k2=4m+1>0
所以m>-
所以m的取值范围:-
<m<0或m>4
则:|PB|-|PA|=2
| 3 |
所以:点p的轨迹是以B、A为焦点的双曲线的左支.
由于|AB|=4
即:c=2
|PB|-|PA|=2
| 3 |
解得:a=
| 3 |
所以双曲线的方程为:
| x2 |
| 3 |
(2)若直线l:y=kx+m(k≠0)与曲线C交于R,S两点
则:
|
整理得:(1-3k2)x2-6kmx-3m2-3=0(1-3k2≠0)
由于△>0
解得:m2+1>3k2①
设R(x1,y1),S(x2,y2)RS的中点坐标为M(x0,y0)
所以x1+x2=
| 6km |
| 1-3k2 |
| -3m2-3 |
| 1-3k2 |
x0=
| x1+x2 |
| 2 |
| 3km |
| 1-3k2 |
| m |
| 1-3k2 |
M(
| 3km |
| 1-3k2 |
| m |
| 1-3k2 |
所以:kMD=
| m+1-3k2 |
| 3km |
|
| RD |
| SD |
kMD•kRS=-1
所以:k•
| m+1-3k2 |
| 3km |
解得:4m+1=3k2代入①得:m2+1>4m+1
解得:m>4或m<0
由于3k2=4m+1>0
所以m>-
| 1 |
| 4 |
所以m的取值范围:-
| 1 |
| 4 |
点评:本题考查的知识要点;双曲线的定义和方程的确定,直线和双曲线的位置关系,中点坐标的应用一元二次方程根和系数的关系,直线垂直的充要条件,及参数的范围的确定.属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
等差数列{an}满足:a4+a6+a8+a10+a12=20,则a9-
a10=( )
| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
函数函数y=
的定义域是( )
| lg(3x+1) | ||
|
| A、∅ | ||
B、(-
| ||
C、(-
| ||
D、(-∞,-
|
如下图2,在平行四边形ABCD中,AD=2AB=2,∠BAC=90°.将△ACD沿AC折起,使得BD=
.在三棱锥D-ABC的四个面中,下列关于垂直关系的叙述错误的是( )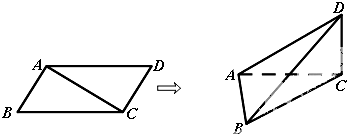
| 5 |

| A、面ABD⊥面BCD |
| B、面ABD⊥面ACD |
| C、面ABC⊥面ACD |
| D、面ABC⊥面BCD |
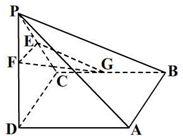 如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,点E,F,G分别为PC,PD,BC的中点.
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,点E,F,G分别为PC,PD,BC的中点.