题目内容
斜线AB与平面α成θ1角，BC在平面α内，∠ABC=θ，AA1⊥平面α，A1为垂足，∠A1BC=θ2，则这三个角之间的关系是 ．
考点：直线与平面所成的角
专题：空间角
分析：过A1，作A1C⊥BC，交BC于点C，连结AC，由三垂线定理，得AC⊥BC，由此能求出cosθ1•cosθ2=
•
=
=cosθ．
| A1B |
| AB |
| BC |
| A1B |
| BC |
| AB |
解答：
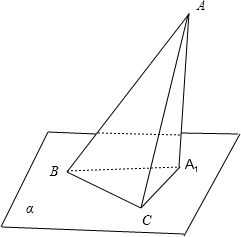解：过A1，作A1C⊥BC，交BC于点C，连结AC，
由三垂线定理，得AC⊥BC，
∴cosθ1=
，cosθ2=
，cosθ=
，
∴cosθ1•cosθ2=
•
=
=cosθ，
∴cosθ=cosθ1•cosθ2．
故答案为：cosθ=cosθ1•cosθ2．
解：过A1，作A1C⊥BC，交BC于点C，连结AC，由三垂线定理，得AC⊥BC，
∴cosθ1=
| A1B |
| AB |
| BC |
| A1B |
| BC |
| AB |
∴cosθ1•cosθ2=
| A1B |
| AB |
| BC |
| A1B |
| BC |
| AB |
∴cosθ=cosθ1•cosθ2．
故答案为：cosθ=cosθ1•cosθ2．
点评：本题考查三个角间的等量关系的求法，是中档题，解题时要认真审题，注意三垂线定理的合理运用．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
已知f（x），g（x）分别是定义在R上的偶函数和奇函数，且f（x）-g（x）=x3+2-x，则f（2）+g（2）=（ ）
| A、4 | B、-4 | C、2 | D、-2 |
某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、π | ||
| B、2π | ||
C、
| ||
D、
|
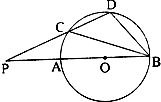如图，从圆O外一点P作圆O的割线 PAB、PCD． AB是圆O的直径，若PA=4，PC=5，CD=3，则∠CBD=