题目内容
已知函数f(x)=ax2-4x+2,函数g(x)=(
)f(x)
(1)若f(2+π+x)=f(2-π-x),求f(x)的解析式;
(2)若g(x)有最大值3,求a的值,并求出g(x)的值域;
(3)已知a≤1,若函数y=f(x)-log2
在区间[1,2]内有且只有一个零点,试确定实数a的取值范围.
| 1 |
| 3 |
(1)若f(2+π+x)=f(2-π-x),求f(x)的解析式;
(2)若g(x)有最大值3,求a的值,并求出g(x)的值域;
(3)已知a≤1,若函数y=f(x)-log2
| x |
| 8 |
考点:函数零点的判定定理,二次函数的性质
专题:函数的性质及应用
分析:(1)f(2+π+x)=f(2-π-x),f(x)的对称轴x=2,求解即可.
(2)函数f(x)=ax2-4x+2的最小值为-1,根据复合函数得出
求解即可.
(3)令r(x)=ax2-4x+5,s(x)=log2x,则可以转化为;函数r(x)与函数s(x)的图象在区间[1,2]上有唯一的交点,分类讨论得出相应的不等式组即可.
(2)函数f(x)=ax2-4x+2的最小值为-1,根据复合函数得出
|
(3)令r(x)=ax2-4x+5,s(x)=log2x,则可以转化为;函数r(x)与函数s(x)的图象在区间[1,2]上有唯一的交点,分类讨论得出相应的不等式组即可.
解答:
解;(1)∵f(2+π+x)=f(2-π-x),
∴f(x)的对称轴x=2,
即
=2,a=1.
∴f(x)=x2-4x+2,
(2)∵函数g(x)=(
)f(x),
g(x)有最大值3,
∴函数f(x)=ax2-4x+2的最小值为-1,
∴
解得:a=
,
∴f(x)=
x2-4x+2=
(x-
)2-1≥-1,
∵函数g(x)=(
)f(x),
∴根据复合函数求解:g(x)的值域(0,3]
(3)∵a≤1,若函数y=f(x)-log2
=ax2-4x+5-log2x
令r(x)=ax2-4x+5,s(x)=log2x,
则可以转化为;函数r(x)与函数s(x)的图象在区间[1,2]上有唯一的交点,
①当a=0时,r(x)=-4x+5,s(x)=log2x,根据 单调性可判断.
∵
∴函数r(x)与函数s(x)的图象在区间[1,2]上有唯一的交点,
②当a≤1,时,抛物线r(x)的开口向下,对称轴x=
<0<1,
∴r(x)=ax2-4x+5在区间[1,2]单调递减,
∵s(x)=log2x在区间[1,2]单调递增,
∴必需
即
得出:-1≤a≤1,由a≤0,
可知;-1≤a<0,
③当0<a≤1时,抛物线r(x)的开口向上,对称轴x=
≥2,
∴r(x)=ax2-4x+5在区间[1,2]单调递减,
s(x)=log2x在区间[1,2]单调递增,
∴必需
即
得出:-1≤a≤1,由根据0<a≤1,
∴0<a≤1
综上所述:实数a的取值范围-1≤a≤1,
∴f(x)的对称轴x=2,
即
| 2 |
| a |
∴f(x)=x2-4x+2,
(2)∵函数g(x)=(
| 1 |
| 3 |
g(x)有最大值3,
∴函数f(x)=ax2-4x+2的最小值为-1,
∴
|
解得:a=
| 4 |
| 3 |
∴f(x)=
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
∵函数g(x)=(
| 1 |
| 3 |
∴根据复合函数求解:g(x)的值域(0,3]
(3)∵a≤1,若函数y=f(x)-log2
| x |
| 8 |
令r(x)=ax2-4x+5,s(x)=log2x,
则可以转化为;函数r(x)与函数s(x)的图象在区间[1,2]上有唯一的交点,
①当a=0时,r(x)=-4x+5,s(x)=log2x,根据 单调性可判断.
∵
|
∴函数r(x)与函数s(x)的图象在区间[1,2]上有唯一的交点,
②当a≤1,时,抛物线r(x)的开口向下,对称轴x=
| 2 |
| a |
∴r(x)=ax2-4x+5在区间[1,2]单调递减,
∵s(x)=log2x在区间[1,2]单调递增,
∴必需
|
即
|
可知;-1≤a<0,
③当0<a≤1时,抛物线r(x)的开口向上,对称轴x=
| 2 |
| a |
∴r(x)=ax2-4x+5在区间[1,2]单调递减,
s(x)=log2x在区间[1,2]单调递增,
∴必需
|
即
|
∴0<a≤1
综上所述:实数a的取值范围-1≤a≤1,
点评:本题考查了函数的单调性,运用判断函数图象的交点问题,转为不等式求解,关键是分类讨论得出等价的不等式组,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )


| A、π | ||
| B、2π | ||
C、
| ||
D、
|
定义在R上的函数f(x)满足f(-x)=f(x),f(x+2)=f(x).当x∈[0,1]时,f(x)=2x2.若在区间[-1,3]上函数g(x)=f(x)-ax-a有3个零点,则实数a的取值范围是( )
A、(0,
| ||
B、(0,
| ||
C、(
| ||
D、(
|
数列{an}中,an+2=an+1-an,a1=2,a2=5,则a2015的值是( )
| A、-2 | B、2 | C、-5 | D、5 |

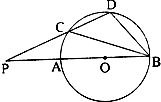 如图,从圆O外一点P作圆O的割线 PAB、PCD. AB是圆O的直径,若PA=4,PC=5,CD=3,则∠CBD=
如图,从圆O外一点P作圆O的割线 PAB、PCD. AB是圆O的直径,若PA=4,PC=5,CD=3,则∠CBD=