题目内容
 如图,在棱长为2的正方体AC′中,E,F为BC和AA′的中点
如图,在棱长为2的正方体AC′中,E,F为BC和AA′的中点(1)求证:FC′⊥平面B′D′E
(2)求A′B与平面B′D′E所成角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)首先建立空间直角坐标系,利用向量的数量积得到直线与直线垂直,进一步利用线面垂直的判定得到结论.
(2)首先求出平面的法向量,进一步利用向量的数量积,及夹角公式求出结果.
(2)首先求出平面的法向量,进一步利用向量的数量积,及夹角公式求出结果.
解答:
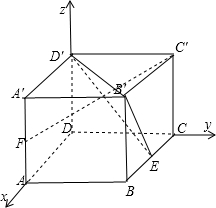 证明:(1)在棱长为2的正方体AC′中,以点D为原点建立空间直角坐标系D-xyz,
证明:(1)在棱长为2的正方体AC′中,以点D为原点建立空间直角坐标系D-xyz,
则:D(0,0,0),E(1,2,0),F((2,0,1),D′(0,0,2),A′(2,0,2),B(2,2,0),C′(0,2,2),B′(2,2,2).
所以:
=(-2,2,1),
=(-2,-2,0),
=(-1,0,-2),
=(0,2,-2)
则:
•
=0
所以:FC′⊥B′D′
同理:
•
=0
所以:FC′⊥B′E
则:FC′⊥平面B′D′E
(2)由于:FC′⊥平面B′D′E
所以:
可以看做是平面B′D′E的法向量,
则:cos<
,
>=
=
则:A′B与平面B′D′E所成角的正弦值为
.
 证明:(1)在棱长为2的正方体AC′中,以点D为原点建立空间直角坐标系D-xyz,
证明:(1)在棱长为2的正方体AC′中,以点D为原点建立空间直角坐标系D-xyz,则:D(0,0,0),E(1,2,0),F((2,0,1),D′(0,0,2),A′(2,0,2),B(2,2,0),C′(0,2,2),B′(2,2,2).
所以:
| FC′ |
| B′D′ |
| B′E |
| A′B |
则:
| FC′ |
| B′D′ |
所以:FC′⊥B′D′
同理:
| FC′ |
| B′E |
所以:FC′⊥B′E
则:FC′⊥平面B′D′E
(2)由于:FC′⊥平面B′D′E
所以:
| FC′ |
则:cos<
| A′B |
| C′F |
| ||||
|
|
| ||
| 6 |
则:A′B与平面B′D′E所成角的正弦值为
| ||
| 6 |
点评:本题考查的知识要点:线面垂直的判定的应用,空间直角坐标系,向量的数量积的应用,法向量的应用,向量的夹角,属于基础题型.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
已知函数f(x)的图象是连续不断的,有如下x,f(x)对应表:函数f(x)在区间[1,6]上零点至少有
( )
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 36.14 | 15.55 | -3.92 | 10.88 | -52.49 | -32.06 |
| A、2个 | B、3个 | C、4个 | D、5个 |
已知数列{an}的通项公式是an=
(n∈N*),若an+an+1=
-3,则n的值是( )
| 1 | ||||
|
| 11 |
| A、10 | B、9 | C、8 | D、6 |
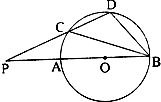 如图,从圆O外一点P作圆O的割线 PAB、PCD. AB是圆O的直径,若PA=4,PC=5,CD=3,则∠CBD=
如图,从圆O外一点P作圆O的割线 PAB、PCD. AB是圆O的直径,若PA=4,PC=5,CD=3,则∠CBD=