题目内容
|x+3|+|x-1|≥6的解集是 ．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：根据绝对值的意义求得不等式|x+2|+|x-1|≤3的解集．
解答：
解：由于|x+3|+|x-1|表示数轴上的x对应点到-3、1对应点的距离之和，
而2和-4对应点到-3、1对应点的距离之和正好等于6，
故|x+3|+|x-1|≥6的解集是{x|x≤-4或 x≥2}，
故答案为：{x|x≤-4或 x≥2}．
而2和-4对应点到-3、1对应点的距离之和正好等于6，
故|x+3|+|x-1|≥6的解集是{x|x≤-4或 x≥2}，
故答案为：{x|x≤-4或 x≥2}．
点评：本题主要考查绝对值的意义，绝对值不等式的解法，属于基础题．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
已知f（x），g（x）分别是定义在R上的偶函数和奇函数，且f（x）-g（x）=x3+2-x，则f（2）+g（2）=（ ）
| A、4 | B、-4 | C、2 | D、-2 |
某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、π | ||
| B、2π | ||
C、
| ||
D、
|
定义在R上的函数f（x）满足f（-x）=f（x），f（x+2）=f（x）．当x∈[0，1]时，f（x）=2x2．若在区间[-1，3]上函数g（x）=f（x）-ax-a有3个零点，则实数a的取值范围是（ ）
A、（0，
| ||
B、（0，
| ||
C、（
| ||
D、（
|
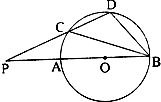如图，从圆O外一点P作圆O的割线 PAB、PCD． AB是圆O的直径，若PA=4，PC=5，CD=3，则∠CBD=
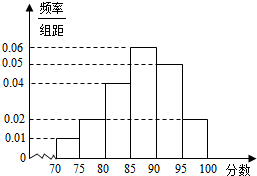某校为规范学生的行为，制定出一套科学有效的“德语百分制量化考核制度”，一领导小组将该校高三年级1200个学生随机编号为1、2、…、1200，现将编号能被30整除的40名学生抽取出来进行座谈，并将他们的考核分分成六段：[70，75），[75，80），[80，85），[85，90），[90，95），[95，100]，统计后得到如图的频率分布直方图：