题目内容
已知函数f(x)=x-alnx(a∈R).
(Ⅰ)当a=2时,求曲线f(x)在x=1处的切线方程;
(Ⅱ)设函数h(x)=f(x)+
,求函数h(x)的单调区间;
(Ⅲ)若g(x)=-
,在[1,e](e=2.71828…)上存在一点x0,使得f(x0)≤g(x0)成立,求a的取值范围.
(Ⅰ)当a=2时,求曲线f(x)在x=1处的切线方程;
(Ⅱ)设函数h(x)=f(x)+
| 1+a |
| x |
(Ⅲ)若g(x)=-
| 1+a |
| x |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求出切点(1,1),求出f′(x)=1-
,然后求解斜率k,即可求解曲线f(x)在点(1,1)处的切线方程.
(Ⅱ)求出函数的定义域,函数的导函数,①a>-1时,②a≤-1时,分别求解函数的单调区间即可.
(Ⅲ)转化已知条件为函数h(x)=x-alnx+
在[1,e]上的最小值[h(x)]min≤0,利用第(Ⅱ)问的结果,通过①a≥e-1时,②a≤0时,③0<a<e-1时,分别求解函数的最小值,推出所求a的范围.
| 2 |
| x |
(Ⅱ)求出函数的定义域,函数的导函数,①a>-1时,②a≤-1时,分别求解函数的单调区间即可.
(Ⅲ)转化已知条件为函数h(x)=x-alnx+
| 1+a |
| x |
解答:
解:(Ⅰ)当a=2时,f(x)=x-2lnx,f(1)=1,切点(1,1),
∴f′(x)=1-
,∴k=f′(1)=1-2=-1,
∴曲线f(x)在点(1,1)处的切线方程为:y-1=-(x-1),即x+y-2=0.
(Ⅱ)h(x)=x-alnx+
,定义域为(0,+∞),h′(x)=1-
-
=
=
,
①当a+1>0,即a>-1时,令h′(x)>0,
∵x>0,∴x>1+a
令h′(x)<0,∵x>0,∴0<x<1+a.
②当a+1≤0,即a≤-1时,h′(x)>0恒成立,
综上:当a>-1时,h(x)在(0,a+1)上单调递减,在(a+1,+∞)上单调递增.
当a≤-1时,h(x)在(0,+∞)上单调递增.
(Ⅲ)由题意可知,在[1,e]上存在一点x0,使得f(x0)≤g(x0)成立,
即在[1,e]上存在一点x0,使得h(x0)≤0,
即函数h(x)=x-alnx+
在[1,e]上的最小值[h(x)]min≤0.
由第(Ⅱ)问,①当a+1≥e,即a≥e-1时,h(x)在[1,e]上单调递减,
∴[h(x)]min=h(e)=e+
-a≤0,∴a≥
,
∵
>e-1,∴a≥
;
②当a+1≤1,即a≤0时,h(x)在[1,e]上单调递增,
∴[h(x)]min=h(1)=1+1+a≤0,
∴a≤-2,
③当1<a+1<e,即0<a<e-1时,∴[h(x)]min=h(1+a)=2+a-aln(1+a)≤0,
∵0<ln(1+a)<1,∴0<aln(1+a)<a,∴h(1+a)>2
此时不存在x0使h(x0)≤0成立.
综上可得所求a的范围是:a≥
或a≤-2.
∴f′(x)=1-
| 2 |
| x |
∴曲线f(x)在点(1,1)处的切线方程为:y-1=-(x-1),即x+y-2=0.
(Ⅱ)h(x)=x-alnx+
| 1+a |
| x |
| a |
| x |
| 1+a |
| x2 |
| x2-ax-(1+a) |
| x2 |
| (x+1)[x-(1+a)] |
| x2 |
①当a+1>0,即a>-1时,令h′(x)>0,
∵x>0,∴x>1+a
令h′(x)<0,∵x>0,∴0<x<1+a.
②当a+1≤0,即a≤-1时,h′(x)>0恒成立,
综上:当a>-1时,h(x)在(0,a+1)上单调递减,在(a+1,+∞)上单调递增.
当a≤-1时,h(x)在(0,+∞)上单调递增.
(Ⅲ)由题意可知,在[1,e]上存在一点x0,使得f(x0)≤g(x0)成立,
即在[1,e]上存在一点x0,使得h(x0)≤0,
即函数h(x)=x-alnx+
| 1+a |
| x |
由第(Ⅱ)问,①当a+1≥e,即a≥e-1时,h(x)在[1,e]上单调递减,
∴[h(x)]min=h(e)=e+
| 1+a |
| e |
| e2+1 |
| e-1 |
∵
| e2+1 |
| e-1 |
| e2+1 |
| e-1 |
②当a+1≤1,即a≤0时,h(x)在[1,e]上单调递增,
∴[h(x)]min=h(1)=1+1+a≤0,
∴a≤-2,
③当1<a+1<e,即0<a<e-1时,∴[h(x)]min=h(1+a)=2+a-aln(1+a)≤0,
∵0<ln(1+a)<1,∴0<aln(1+a)<a,∴h(1+a)>2
此时不存在x0使h(x0)≤0成立.
综上可得所求a的范围是:a≥
| e2+1 |
| e-1 |
点评:本题考查函数的导数的综合应用,曲线的切线方程函数的单调性以及函数的最值的应用,考查分析问题解决问题得到能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
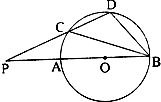 如图,从圆O外一点P作圆O的割线 PAB、PCD. AB是圆O的直径,若PA=4,PC=5,CD=3,则∠CBD=
如图,从圆O外一点P作圆O的割线 PAB、PCD. AB是圆O的直径,若PA=4,PC=5,CD=3,则∠CBD=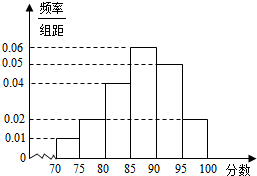 某校为规范学生的行为,制定出一套科学有效的“德语百分制量化考核制度”,一领导小组将该校高三年级1200个学生随机编号为1、2、…、1200,现将编号能被30整除的40名学生抽取出来进行座谈,并将他们的考核分分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100],统计后得到如图的频率分布直方图:
某校为规范学生的行为,制定出一套科学有效的“德语百分制量化考核制度”,一领导小组将该校高三年级1200个学生随机编号为1、2、…、1200,现将编号能被30整除的40名学生抽取出来进行座谈,并将他们的考核分分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100],统计后得到如图的频率分布直方图: