题目内容
14.若a>b,ab=1,则$M=\frac{{{a^2}+{b^2}}}{a-b}$的取值范围是[2$\sqrt{2}$,+∞).分析 运用配方,结合a-b>0,ab=1,运用基本不等式即可得到所求范围.
解答 解:若a>b,ab=1,则$M=\frac{{{a^2}+{b^2}}}{a-b}$
=$\frac{(a-b)^{2}+2ab}{a-b}$=(a-b)+$\frac{2}{a-b}$
≥2$\sqrt{(a-b)•\frac{2}{a-b}}$=2$\sqrt{2}$,
当且仅当a-b=$\sqrt{2}$时取得等号.
故答案为:[2$\sqrt{2}$,+∞).
点评 本题考查基本不等式的运用:求范围,考查变形和运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.设{an}是等差数列,a1+a3+a5=9,a1=9.则这个数列的公差等于( )
| A. | 1 | B. | 2 | C. | -3 | D. | -4 |
19. 本学期王老师任教两个平行班高三A班、高三B班,两个班都是50个学生,如图图反映的是两个班在本学期5次数学测试中的班级平均分对比,根据图表,不正确的结论是( )
本学期王老师任教两个平行班高三A班、高三B班,两个班都是50个学生,如图图反映的是两个班在本学期5次数学测试中的班级平均分对比,根据图表,不正确的结论是( )
 本学期王老师任教两个平行班高三A班、高三B班,两个班都是50个学生,如图图反映的是两个班在本学期5次数学测试中的班级平均分对比,根据图表,不正确的结论是( )
本学期王老师任教两个平行班高三A班、高三B班,两个班都是50个学生,如图图反映的是两个班在本学期5次数学测试中的班级平均分对比,根据图表,不正确的结论是( )| A. | A班的数学成绩平均水平好于B班 | |
| B. | B班的数学成绩没有A班稳定 | |
| C. | 下次考试B班的数学平均分要高于A班 | |
| D. | 在第1次考试中,A、B两个班的总平均分为98 |
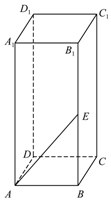 如图所示,长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.过点A1,D1,E的平面α与此长方体的面相交,交线围成一个四边形.
如图所示,长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.过点A1,D1,E的平面α与此长方体的面相交,交线围成一个四边形.