题目内容

3．用秦九韶算法求多项式f（x）=x6-5x5+6x4-3x3+1.8x2+0.35x+2，在x=-1的值时，v2的值是12．

分析 首先把一个n次多项式f（x）写成（…（（a[n]x+a[n-1]）x+a[n-2]）x+…+a[1]）x+a[0]的形式，然后化简，求n次多项式f（x）的值就转化为求n个一次多项式的值，求出V3的值．

解答 解：∵f（x）=x6-5x5+6x4-3x3+1.8x2+0.35x+2=（（x-5）x+6）x-3）x+1.8）x+0.35）x+2，
∴v0=a6=1，
v1=v0x+a5=1×（-1）-5=-6，
v2=v1x+a4=-6×（-1）+6=12，
∴v2的值为12，
故答案为12．

点评 本题考查排序问题与算法的多样性，通过数学上的算法，写成程序，然后求解，属于中档题．

练习册系列答案
相关题目
13．对于曲线C：f（x，y）=0，若存在非负实数M和m，使得曲线C上任意一点P（x，y），m≤|OP|≤M恒成立（其中O为坐标原点），则称曲线C为有界曲线，且称M的最小值M0为曲线C的外确界，m的最大值m0为曲线C的内确界．
（1）写出曲线x+y=1（0＜x＜4）的外确界M0与内确界m0；
（2）曲线y2=4x与曲线（x-1）2+y2=4是否为有界曲线？若是，求出其外确界与内确界；若不是，请说明理由；
（3）已知曲线C上任意一点P（x，y）到定点F1（-1，0），F2（1，0）的距离之积为常数a（a＞0），求曲线C的外确界与内确界．
14．若a＞b，ab=1，则$M=\frac{{{a^2}+{b^2}}}{a-b}$的取值范围是[2$\sqrt{2}$，+∞）．
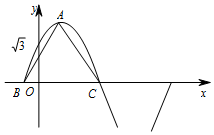11．已知函数$f（x）=Asin（{ωx+φ}）（{A＞0\;，\;\;ω＞0\;，\;\;|φ|＜\frac{π}{2}}）$在一个周期内的图象如图所示，图象过点$（{0\;，\;\;\sqrt{3}}）$，A为图象的最高点，B，C为图象与x轴的交点，且△ABC为高为$2\sqrt{3}$的正三角形．
（1）求A，ω，φ的值；
（2）当$x∈[{-\frac{2}{3}\;，\;\;\frac{4}{3}}]$时，求函数f（x）的值域；
（3）将y=f（x）的图象所在点向左平行移动θ（θ＞0）的单位长度，得到y=g（x）的图象．若y=g（x）的图象的一个对称中心为$（{\frac{2}{3}\;，\;\;0}）$，求θ的最小值．
18．已知函数$f（n）=\left\{\begin{array}{l}n-3（{n≥10}）\;，\;\;\\ f[{f（{n+5}）}]（{n＜10}）\;，\;\;\end{array}\right.$其中n∈N，则f（9）等于（　　）
A．4B．6C．7D．8
8．已知对任意x1、x2∈（0，+∞）且x1＜x2，幂函数$f（x）={x^{-\frac{p^2}{2}+p+\frac{3}{2}}}$（p∈Z），满足f（x1）＜f（x2），并且对任意的x∈R，f（x）-f（-x）=0．
（1）求p的值，并写出函数f（x）的解析式；
（2）对于（1）中求得的函数f（x），设g（x）=-qf（x）+（2q-1）x+1，问：是否存在负实数q，使得g（x）在（-∞，-4）上是减函数，且在[-4，+∞）上是增函数？若存在，求出q的值；若不存在，说明理由．
15．已知数列{an}中，a1=1，a2=6，an+2=an+1-an，则a2016=-5．
12．函数$f（x）=sinx+\sqrt{3}•cosx$，若存在锐角θ满足f（θ）=2，则θ=$\frac{π}{6}$．
13．已知集合P=（-∞，0]∪（3，+∞），Q={0，1，2，3}，则（∁RP）∩Q=（　　）
A．{0，1}B．{0，1，2}C．{1，2，3}D．{x|0≤x＜3}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网