题目内容
6．我们国家正处于老龄化社会中，老有所依也是政府的民生工程．某市共有户籍人口400万，其中老人（年龄60岁及以上）人数约有66万，为了了解老人们的健康状况，政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估，健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级，并以80岁为界限分成两个群体进行统计，样本分布被制作成如下图表：
（Ⅰ）若采用分层抽样的方法再从样本中的不能自理的老人中抽取16人进一步了解他们的生活状况，则两个群体中各应抽取多少人？
（Ⅱ）估算该市80岁及以上长者占全市户籍人口的百分比；
（Ⅲ）政府计划为80岁及以上长者或生活不能自理的老人每人购买1000元/年的医疗保险，为其余老人每人购买600元/年的医疗保险，不可重复享受，试估计政府执行此计划的年度预算．
分析 （Ⅰ）从图表中求出不能自理的80岁及以上长者占比，由此能求出抽取16人中不能自理的80岁及以上长者人数为．
（Ⅱ）求出在600人中80岁及以上长者在老人中占比，用样本估计总体，能求出80岁及以上长者占户籍人口的百分比．
（Ⅲ）先计算抽样的600人的预算，用样本估计总体，从而能估计政府执行此计划的年度预算．
解答 解：（Ⅰ）数据整理如下表：
| 健康状况 | 健康 | 基本健康 | 不健康尚能自理 | 不能自理 |
| 80岁及以上 | 20 | 45 | 20 | 15 |
| 80岁以下 | 200 | 225 | 50 | 25 |
故抽取16人中不能自理的80岁及以上长者人数为16×$\frac{3}{8}$=6，能自理的80岁及以上长者人数为10．
（Ⅱ）在600人中80岁及以上长者在老人中占比为：$\frac{15+20+45+20}{600}$=$\frac{1}{6}$，80岁及以上长者有$66×\frac{1}{6}$=11，
用样本估计总体，80岁及以上长者占户籍人口的百分比为$\frac{11}{400}×100%$=2.75%．
（Ⅲ）先计算抽样的600人的预算，其中享受1000元/年的人数为14+25+20+45+20=125人，享受600元/年的人数为600-125=475人，预算为125×1000+475×600=41×104元，
用样本估计总体，全市老人的总预算为$\frac{66×1{0}^{4}}{600}$×41×104=4.51×108元．
政府执行此计划的年度预算约为4.51亿元．
点评 本题考查分表图、分层抽样的应用，考查学生的计算能力，是中档题．
练习册系列答案
目标测试系列答案
相关题目
16．与直线 $y=\frac{1}{2}x+1$垂直，且过（2，0）点的直线方程是（ ）
| A． | y=-2x+4 | B． | $y=\frac{1}{2}x-1$ | C． | y=-2x-4 | D． | $y=\frac{1}{2}x-4$ |
17．已知f（x）是定义在R上的不恒为0的函数，若对于任意的实数a、b都满足f（ab）=af（b）+bf（a），则函数f（x）（ ）
| A． | 是奇函数 | B． | 是偶函数 | ||
| C． | 既是奇函数又是偶函数 | D． | 既不是奇函数又不是偶函数 |
1．对任意a∈R，曲线y=ex（x2+ax+1-2a）在点P（0，1-2a）处的切线l与圆C：（x-1）2+y2=16的位置关系是（ ）
| A． | 相交 | B． | 相切 | C． | 相离 | D． | 以上均有可能 |
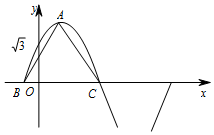已知函数$f（x）=Asin（{ωx+φ}）（{A＞0\;，\;\;ω＞0\;，\;\;|φ|＜\frac{π}{2}}）$在一个周期内的图象如图所示，图象过点$（{0\;，\;\;\sqrt{3}}）$，A为图象的最高点，B，C为图象与x轴的交点，且△ABC为高为$2\sqrt{3}$的正三角形．