题目内容
4.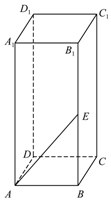 如图所示,长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.过点A1,D1,E的平面α与此长方体的面相交,交线围成一个四边形.
如图所示,长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.过点A1,D1,E的平面α与此长方体的面相交,交线围成一个四边形.(Ⅰ)请在图中作出此四边形(简要说明画法);
(Ⅱ)证明AE⊥平面α.
分析 (Ⅰ)取CC1中点F,连结A1E,EF,FD1,则四边形A1EFD1即为所求四边形.
(Ⅱ)推导出A1E⊥AE,AE⊥A1D1,由此能证明AE⊥平面α.
解答 解:(Ⅰ)取CC1中点F,连结A1E,EF,FD1,
则四边形A1EFD1即为所求四边形.(其它做法请酌情给分)…(4分)
证明:(Ⅱ)∵E为BB1中点,∴B1E=BE=1,A1E=AE=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
又∵AA1=2,∴$A{{A}_{1}}^{2}$=${A}_{1}{E}^{2}+A{E}^{2}$,
∴A1E⊥AE,…(6分)
又∵A1D1⊥平面ABB1A1,AE?平面ABB1A1
∴AE⊥A1D1,…(8分)
又∵A1E?平面A1EFD1,A1D1?平面A1EFD1,A1E∩A1D1=A1,
∴AE⊥平面A1EFD1,∴AE⊥平面α.…(12分)
点评 本题考查图形有画法,考查线面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知集合A={x|$\sqrt{2x-1}$>1},则∁RA=( )
| A. | {x|x>1} | B. | {x|x≥$\frac{1}{2}$} | C. | {x|x≤1} | D. | {x|x<$\frac{1}{2}$} |
9.已知a=0.78,b=80.7,c=log0.78,则a、b、c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
16.与直线 $y=\frac{1}{2}x+1$垂直,且过(2,0)点的直线方程是( )
| A. | y=-2x+4 | B. | $y=\frac{1}{2}x-1$ | C. | y=-2x-4 | D. | $y=\frac{1}{2}x-4$ |