题目内容
4.已知双曲线Γ:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0),直线l:x+y-2=0,F1,F2为双曲线Γ的两个焦点,l与双曲线Γ的一条渐近线平行且过其中一个焦点.(1)求双曲线Γ的方程;
(2)设Γ与l的交点为P,求∠F1PF2的角平分线所在直线的方程.
分析 (1)依题意,双曲线的渐近线方程为y=±x,焦点坐标为F1(-2,0),F2(2,0),即可求双曲线Γ的方程;
(2)设Γ与l的交点为P,求出P的坐标,利用夹角公式,即可求∠F1PF2的角平分线所在直线的方程.
解答 解:(1)依题意,双曲线的渐近线方程为y=±x,焦点坐标为F1(-2,0),F2(2,0),
∴双曲线方程为x2-y2=2;
(2)$\left\{\begin{array}{l}{x^2}-{y^2}=2\\ x+y-2=0\end{array}\right.⇒P(\frac{3}{2},\frac{1}{2})$,显然∠F1PF2的角平分线所在直线斜率k存在,且k>0,${k_{P{F_1}}}=\frac{1}{7}$,${k_{P{F_2}}}=-1$,于是$|\frac{{{k_{P{F_1}}}-k}}{{1+{k_{P{F_1}}}k}}|=|\frac{{{k_{P{F_2}}}-k}}{{1+{k_{P{F_2}}}k}}|⇒k=3$.∴$y-\frac{1}{2}=3(x-\frac{3}{2})⇒3x-y-4=0$为所求.
点评 本题考查双曲线的方程与性质,考查直线的夹角公式的运用,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
19.已知集合A={x|x>-1},则下列选项正确的是( )
| A. | 0⊆A | B. | {0}⊆A | C. | ∅∈A | D. | {0}∈A |
9.设$a=\frac{1}{{\sqrt{2}}}({sin56°-cos56°})$,b=cos50°•cos128°+cos40°•cos38°,$c=\frac{1}{2}({cos80°-2{{cos}^2}50°+1})$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
13.已知集合P=(-∞,0]∪(3,+∞),Q={0,1,2,3},则(∁RP)∩Q=( )
| A. | {0,1} | B. | {0,1,2} | C. | {1,2,3} | D. | {x|0≤x<3} |
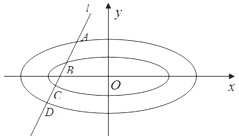 已知椭圆C1,C2均为中心在原点,焦点在x轴上的椭圆,离心率均为$\frac{{\sqrt{2}}}{2}$,其中C1的焦点坐标分别为(-1,0),(1,0),C2的左右顶点坐标为(-2,0),(2,0).
已知椭圆C1,C2均为中心在原点,焦点在x轴上的椭圆,离心率均为$\frac{{\sqrt{2}}}{2}$,其中C1的焦点坐标分别为(-1,0),(1,0),C2的左右顶点坐标为(-2,0),(2,0).