题目内容
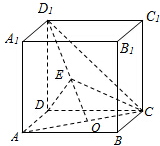 如图,在正方体ABCD-A1B1C1D1中,O是AC的中点,E是线段D1O上一点,且|D1E|=λ|EO|.
如图,在正方体ABCD-A1B1C1D1中,O是AC的中点,E是线段D1O上一点,且|D1E|=λ|EO|.(1)求证:DB1⊥平面CD1O;
(2)若平面CDE⊥平面CD1O,求λ的值.
考点:平面与平面垂直的判定,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由线面垂直得D1D⊥AC,又AC⊥BD,从而AC⊥平面D1DBB1,进而AC⊥B1D,同理可证D1C⊥B1D,由此能证明B1D⊥平面CD1O,.
(2)由已知得AC⊥DE,要使平面CDE⊥平面CD1O,只需DE⊥平面CD1O,即需DE⊥D1O,设D1D=2,则DO=
,由此能求出
=2,由|D1E|=λ|EO|,得λ=2.
(2)由已知得AC⊥DE,要使平面CDE⊥平面CD1O,只需DE⊥平面CD1O,即需DE⊥D1O,设D1D=2,则DO=
| 2 |
| D1E |
| EO |
解答:
 解:(1)证明:∵D1D⊥平面ABCD,∴D1D⊥AC,
解:(1)证明:∵D1D⊥平面ABCD,∴D1D⊥AC,
又AC⊥BD,∴AC⊥平面D1DBB1,∴AC⊥B1D,
同理可证D1C⊥B1D,∴B1D⊥平面CD1O.
(2)解:∵O为AC的中点,∴在△D1AC中,D1O⊥AC,
又∵D1D⊥AC,∴AC⊥平面D1OD,∴AC⊥DE,
要使平面CDE⊥平面CD1O,只需DE⊥平面CD1O,
即需DE⊥D1O,(∵PE⊥AC,∴DE⊥平面CD1O),
设D1D=2,则DO=
,∴在Rt△D1DO中,OD1=
,
∴DE=
=
,
∴D1E=
=
,
∴EO=
,∴
=2,∵|D1E|=λ|EO|,∴λ=2.
 解:(1)证明:∵D1D⊥平面ABCD,∴D1D⊥AC,
解:(1)证明:∵D1D⊥平面ABCD,∴D1D⊥AC,又AC⊥BD,∴AC⊥平面D1DBB1,∴AC⊥B1D,
同理可证D1C⊥B1D,∴B1D⊥平面CD1O.
(2)解:∵O为AC的中点,∴在△D1AC中,D1O⊥AC,
又∵D1D⊥AC,∴AC⊥平面D1OD,∴AC⊥DE,
要使平面CDE⊥平面CD1O,只需DE⊥平面CD1O,
即需DE⊥D1O,(∵PE⊥AC,∴DE⊥平面CD1O),
设D1D=2,则DO=
| 2 |
| 6 |
∴DE=
2
| ||
|
2
| ||
| 3 |
∴D1E=
4-(
|
2
| ||
| 3 |
∴EO=
| ||
| 3 |
| D1E |
| EO |
点评:本题考查线面垂直的证明,考查使得面面垂直的实数值的求法,考查方程思想、等价转化思想等数学思想方法和学生的空间想象能力、逻辑推理能力和运算求解能力,是中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
已知集合S={x|3x+a=0},如果1∈S,那么a的值为( )
| A、-3 | B、-1 | C、1 | D、3 |
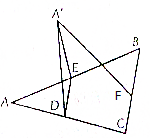 如图所示,在平面α内有一边长为a的等边△ABC,在△ABC中,DE∥BC,沿DE将△ABC折起,使它和△ABC所在半平面成60°的二面角,问直线DE取在何处,折起后的三角形顶点A(可记A′)到BC边的距离最短,最短距离是多少?
如图所示,在平面α内有一边长为a的等边△ABC,在△ABC中,DE∥BC,沿DE将△ABC折起,使它和△ABC所在半平面成60°的二面角,问直线DE取在何处,折起后的三角形顶点A(可记A′)到BC边的距离最短,最短距离是多少?