题目内容
已知集合S={x|3x+a=0},如果1∈S,那么a的值为( )
| A、-3 | B、-1 | C、1 | D、3 |
考点:元素与集合关系的判断
专题:集合
分析:根据集合S={x|3x+a=0},且1∈S,知道1满足等式,解此方程即可求得实数a的值.
解答:
解:∵S={x|3x+a=0},且1∈S,
∴3×1+a=0,
解得:a=-3.
故选:A.
∴3×1+a=0,
解得:a=-3.
故选:A.
点评:此题考查元素与集合之间的关系,以及分式不等式的求解,对题意的正确理解和转化是解决此题的关键,属基础题.

练习册系列答案
相关题目
己知命题p:“a>b”是“2a>2b”的充要条件;q:?x∈R,|x+l|≤x,则( )
| A、¬p∨q为真命题 |
| B、p∧¬q为假命题 |
| C、p∧q为真命题 |
| D、p∨q为真命题 |
设F1、F2为椭圆C:
+
=1(a>b>0)的左、右焦点,直线l过焦点F2且与椭圆交于A,B两点,若△ABF1构成以A为直角顶点的等腰直角三角形,设椭圆离心率为e,则e2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、2-
| ||
B、3-
| ||
C、11-6
| ||
D、9-6
|
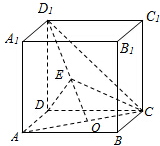 如图,在正方体ABCD-A1B1C1D1中,O是AC的中点,E是线段D1O上一点,且|D1E|=λ|EO|.
如图,在正方体ABCD-A1B1C1D1中,O是AC的中点,E是线段D1O上一点,且|D1E|=λ|EO|.