题目内容
对?n∈N*,13+23+…+(n-1)3<n4•S<13+23+…+n3恒成立,则S= .
考点:数列与不等式的综合
专题:点列、递归数列与数学归纳法
分析:由13+23+…+n3=
n2(n+1)2,把对?n∈N*,13+23+…+(n-1)3<n4•S<13+23+…+n3恒成立转化为
(n-1)2n2<n4S<
n2(n+1)2恒成立,两边同时除以4n2后可得满足不等式恒成立的S的值.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:首先证明13+23+…+n3=
n2(n+1)2.
下面利用数学归纳法证明:
①当n=1时,等式左边=13=1,右边=
×12×(1+1)2=1,左边=右边,等式成立;
②假设当n=k时结论成立,即13+23+…+k3=
k2(k+1)2,
那么,当n=k+1时,13+23+…+k3+(k+1)3=
k2(k+1)2+(k+1)3=
(k+1)2(k2+4k+4)=
(k+1)2(k+2)2.
即n=k+1时等式成立.
综①②所述,等式13+23+…+k3=
k2(k+1)2对于任意的n∈N*都成立.
则对?n∈N*,13+23+…+(n-1)3<n4•S<13+23+…+n3恒成立,可转化为
(n-1)2n2<n4S<
n2(n+1)2恒成立.
即
(
)2<S<
(
)2,∴S=
.
故答案为:
.
| 1 |
| 4 |
下面利用数学归纳法证明:
①当n=1时,等式左边=13=1,右边=
| 1 |
| 4 |
②假设当n=k时结论成立,即13+23+…+k3=
| 1 |
| 4 |
那么,当n=k+1时,13+23+…+k3+(k+1)3=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
即n=k+1时等式成立.
综①②所述,等式13+23+…+k3=
| 1 |
| 4 |
则对?n∈N*,13+23+…+(n-1)3<n4•S<13+23+…+n3恒成立,可转化为
| 1 |
| 4 |
| 1 |
| 4 |
即
| 1 |
| 4 |
| n-1 |
| n |
| 1 |
| 4 |
| n+1 |
| n |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题是数列与不等式的综合题,考查了数学转化思想方法,解答此题的关键在于运用等式13+23+…+n3=
n2(n+1)2把原不等式转化,是中档题.
| 1 |
| 4 |

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
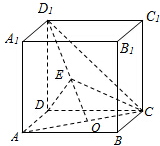 如图,在正方体ABCD-A1B1C1D1中,O是AC的中点,E是线段D1O上一点,且|D1E|=λ|EO|.
如图,在正方体ABCD-A1B1C1D1中,O是AC的中点,E是线段D1O上一点,且|D1E|=λ|EO|. 已知正四面体ABCD中,棱长为a,M、N分别为BC、AD的中点.求:
已知正四面体ABCD中,棱长为a,M、N分别为BC、AD的中点.求: