题目内容
设F1（-5，0）、F2（5，0）、M0（-2，0），曲线C满足条件|PF1|-|PF2|=8的动点P的轨迹，则|PM0|的最小值为 ．
考点：双曲线的简单性质,轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：求出双曲线的方程，即可求出|PM0|的最小值．
解答：
解：由题意，P的轨迹是以F1（-5，0）、F2（5，0）为焦点的双曲线的右支，且c=5，a=4，b=3，
∴双曲线的方程为
-
=1（x≥4），
∵M0（-2，0），
∴|PM0|的最小值为2．
故答案为：2．
∴双曲线的方程为
| x2 |
| 16 |
| y2 |
| 9 |
∵M0（-2，0），
∴|PM0|的最小值为2．
故答案为：2．
点评：本题考查|PM0|的最小值，考查双曲线的定义与方程，确定双曲线的方程是关键．
练习册系列答案
相关题目
直线y=a分别与曲线y=2（x+1），y=x+lnx交于A、B，则|AB|的最小值为（ ）
| A、3 | ||||
| B、2 | ||||
C、
| ||||
D、
|
己知命题p：“a＞b”是“2a＞2b”的充要条件；q：?x∈R，|x+l|≤x，则（ ）
| A、￢p∨q为真命题 |
| B、p∧￢q为假命题 |
| C、p∧q为真命题 |
| D、p∨q为真命题 |
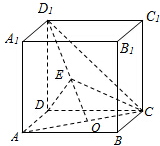如图，在正方体ABCD-A1B1C1D1中，O是AC的中点，E是线段D1O上一点，且|D1E|=λ|EO|．