题目内容
若函数f（x）=x3+x2+mx+1是R上的单调增函数，则实数m的取值范围是（ ）
A、[
| ||
B、（-
| ||
C、（-∞，
| ||
D、（-∞，
|
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：求函数的导数，根据函数单调性和导数之间的关系转化为f′（x）≥0恒成立，解不等式即可得到结论．
解答：
解：要使函数f（x）=x3+x2+mx+1是R上的单调增函数，
则f′（x）=3x2+2x+m≥0恒成立，
即判别式△=4-4×3m≤0，
解得m≥
，
故实数m的取值范围是[
，+∞），
故选：A．
则f′（x）=3x2+2x+m≥0恒成立，
即判别式△=4-4×3m≤0，
解得m≥
| 1 |
| 3 |
故实数m的取值范围是[
| 1 |
| 3 |
故选：A．
点评：本题主要考查函数单调性和导数之间的关系，根据函数的单调性转化为f′（x）≥0恒成立是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
椭圆
+
=1的焦点为F1，F2，P为椭圆上的点，已知∠F1PF2=90°，则△PF1F2的面积为（ ）
| x2 |
| 25 |
| y2 |
| 9 |
| A、9 | B、12 |
| C、18 | D、以上均不对 |
过点P（-2，1）且方向向量为
=（-2，3）的直线方程为（ ）
| n |
| A、3x+2y-8=0 |
| B、3x+2y+4=0 |
| C、2x+3y+1=0 |
| D、2x+3y-7=0 |
过正三棱锥的侧棱与底面中心作截面，如果截面是等腰三角形，则侧面与底面所成角的余弦值是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
在空间直角坐标系中，定义：平面α的一般方程为：Ax+By+Cz+D=0（A，B，C，D∈R，且A，B，C不同时为零），点P（x0，y0，z0）到平面α的距离为：d=
，则在底面边长与高都为2的正四棱锥中，底面中心O到侧面的距离等于（ ）
| |Ax0+By0+Cz0+D| | ||
|
A、
| ||||
B、
| ||||
| C、2 | ||||
| D、5 |
若向量
=（1，3），
=（x，-1）的夹角为钝角，则实数x的取值范围为（ ）
| a |
| b |
| A、（-∞，3） | ||||
| B、（3，+∞） | ||||
C、（-∞，
| ||||
D、（-∞，-
|
| ∫ |
0 |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、1 |
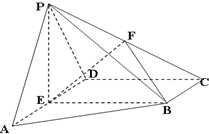已知在四棱锥P-ABCD中，AD∥BC，AD⊥CD，PA=PD=AD=2BC=2CD，E，F分别是AD，PC的中点．