题目内容
过正三棱锥的侧棱与底面中心作截面,如果截面是等腰三角形,则侧面与底面所成角的余弦值是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:二面角的平面角及求法
专题:综合题,空间角
分析:延长BO交AC于D,则D为AC中点,∠SDB为侧面和底面所成角的平面角.截面△SBD分SD=BD,SB=BD 两种情况求解.
解答:
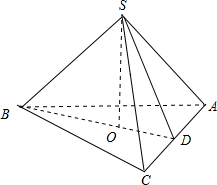 解:延长BO交AC于D,则D为AC中点.截面为△SBD.
解:延长BO交AC于D,则D为AC中点.截面为△SBD.
由正棱锥的性质,SO⊥面ABC,SD⊥AC,BD⊥AC,∠SDB为侧面和底面所成角的平面角.设底面边长BC=2.易知SB≠SD.
(1)若SD=BD,则SC=BC,正三棱锥S-ABC为正四面体.
BD=
=
,
在△SDB中,由余弦定理得cos∠SDB=
=
.
(2)若SB=BD=
,
在RT△SDA中,SD=
=
,
在△SDB中,由余弦定理得cos∠SDB=
=
.
故选:D.
 解:延长BO交AC于D,则D为AC中点.截面为△SBD.
解:延长BO交AC于D,则D为AC中点.截面为△SBD.由正棱锥的性质,SO⊥面ABC,SD⊥AC,BD⊥AC,∠SDB为侧面和底面所成角的平面角.设底面边长BC=2.易知SB≠SD.
(1)若SD=BD,则SC=BC,正三棱锥S-ABC为正四面体.
BD=
| BC2-CD2 |
| 3 |
在△SDB中,由余弦定理得cos∠SDB=
| 3+3-4 | ||||
2×
|
| 1 |
| 3 |
(2)若SB=BD=
| 3 |
在RT△SDA中,SD=
| SA2-AD2 |
| 2 |
在△SDB中,由余弦定理得cos∠SDB=
| 3+2-3 | ||||
2×
|
| ||
| 6 |
故选:D.
点评:本题考查了正棱锥的性质,面面角的计算.考查空间想象能力、计算、推理论证能力.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
cos24°cos36°-sin24°sin36°的值等于( )
A、
| ||||
B、-
| ||||
C、
| ||||
| D、cos12° |
已知向量
,
满足
•
=0,|
|=1,|
|=2,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、0 | ||
| B、1 | ||
| C、2 | ||
D、
|
椭圆
+
=1的焦距是2,那么椭圆的长轴长为( )
| x2 |
| 4 |
| y2 |
| k |
A、2或2
| ||
B、2或2
| ||
C、4或2
| ||
D、4或2
|
阅读如图所示的程序框图,若输入的x=log (a2+2)
,则输出的值为( )

| 1 |
| 2 |

| A、1 | B、0 |
| C、1或0 | D、与a的大小有关 |
若函数f(x)=x3+x2+mx+1是R上的单调增函数,则实数m的取值范围是( )
A、[
| ||
B、(-
| ||
C、(-∞,
| ||
D、(-∞,
|