题目内容
某产品经过4次革新后，成本由原来的120元下降到70元．若每次革新后，成本下降的百分率相同，那么每次革新后成本下降的百分率为 （精确到0.1%）．
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：设每次降价的百分率为x，（1-x）4为四次降价的百分率，120降至70就是方程的平衡条件，列出方程求解即可．
解答：
解：设每次降价的百分率为x．则
120×（1-x）4=70
解得x=12.6%．
故答案为：12.6%；
120×（1-x）4=70
解得x=12.6%．
故答案为：12.6%；
点评：此题主要考查了等比数列的应用，关键是根据题意找到等式两边的平衡条件，这种价格问题主要解决价格变化前后的平衡关系，列出方程，解答即可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
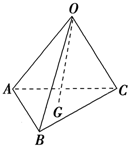如图，在三棱锥O-ABC中，G是△ABC的重心，若| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| OG |
A、
| ||||||
B、
| ||||||
| C、a+b+c | ||||||
| D、3a+3b+3c |
若圆x2+y2-4x-4y-10=0上至少有三个不同点到直线l：ax+by=0的距离为2
，则直线l的斜率的取值范围是（ ）
| 2 |
A、[2-
| ||||||
B、[2-
| ||||||
C、[
| ||||||
| D、[0，+∞） |
过抛物线y2=10x的焦点作一条直线与抛物线相交于A、B两点，它们的横坐标之和等于5，则这样的直线（ ）
| A、有且仅有一条 |
| B、有且仅有两条 |
| C、有无穷多条 |
| D、不存在 |
