题目内容
若圆x2+y2-4x-4y-10=0上至少有三个不同点到直线l:ax+by=0的距离为2
,则直线l的斜率的取值范围是( )
| 2 |
A、[2-
| ||||||
B、[2-
| ||||||
C、[
| ||||||
| D、[0,+∞) |
考点:直线和圆的方程的应用
专题:计算题,圆锥曲线中的最值与范围问题
分析:求出圆心(2,2)与半径3
,则圆x2+y2-4x-4y-10=0上至少有三个不同点到直线l:ax+by=0的距离为2
可化为圆心到直线l:ax+by=0的距离d≤
;从而求直线l的斜率的取值范围.
| 2 |
| 2 |
| 2 |
解答:
解:圆x2+y2-4x-4y-10=0可化为
(x-2)2+(y-2)2=18,
则圆心为(2,2),半径为3
;
则由圆x2+y2-4x-4y-10=0上至少有三个不同点到直线l:ax+by=0的距离为2
可得,
圆心到直线l:ax+by=0的距离d≤3
-2
=
;
即
≤
,
则a2+b2+4ab≤0,
若a=0,则b=0,故不成立,
故a≠0,则上式可化为
1+(
)2+4
≤0,
由直线l的斜率k=-
,
则上式可化为1+k2-4k≤0,
则∈[2-
,2+
],
故选B.
(x-2)2+(y-2)2=18,
则圆心为(2,2),半径为3
| 2 |
则由圆x2+y2-4x-4y-10=0上至少有三个不同点到直线l:ax+by=0的距离为2
| 2 |
圆心到直线l:ax+by=0的距离d≤3
| 2 |
| 2 |
| 2 |
即
| |2a+2b| | ||
|
| 2 |
则a2+b2+4ab≤0,
若a=0,则b=0,故不成立,
故a≠0,则上式可化为
1+(
| b |
| a |
| b |
| a |
由直线l的斜率k=-
| b |
| a |
则上式可化为1+k2-4k≤0,
则∈[2-
| 3 |
| 3 |
故选B.
点评:本题考查了直线与圆上点的距离的应用,题意中将圆x2+y2-4x-4y-10=0上至少有三个不同点到直线l:ax+by=0的距离为2
可化为圆心到直线l:ax+by=0的距离d≤
;是本题解答的关键,属于中档题.
| 2 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若y=f(x)的定义域是[0,2],则函数f(x+1)的定义域是( )
| A、[-1,1] | ||||
B、[
| ||||
C、[
| ||||
D、[0,
|
已知函数f(x)=
,记f1(x)=f(x),f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,则f2014(10)=( )
|
| A、10 | B、lg110 | C、0 | D、1 |
在数列{an}中,若a1=1,an-an-1=n,(n≥2),则该数列的通项an=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
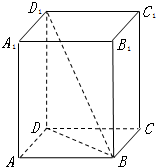 如图,长方体ABCD-A1B1C1D1中,ABCD是边长为1的正方形,D1B=
如图,长方体ABCD-A1B1C1D1中,ABCD是边长为1的正方形,D1B=