题目内容

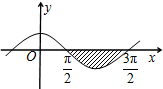
如图，阴影区域是由函数y=cosx的一段图象与x轴围成的封闭图形，则该阴影区域的面积是
 
．
考点：定积分
专题：导数的综合应用
分析：由题意，利用定积分的几何意义，所求阴影区域的面积是S=-
∫
3π
2
π
2
cosxdx，即可得出结论．
解答： 解：由题意，阴影区域的面积是S=-
∫
3π
2
π
2
cosxdx=-sinx
|
3π
2
π
2
=2．
故答案为：2．
点评：本题考查了运用定积分求曲边梯形的面积，属于基础题．
练习册系列答案
相关题目
某产品经过4次革新后，成本由原来的120元下降到70元．若每次革新后，成本下降的百分率相同，那么每次革新后成本下降的百分率为
 
 （精确到0.1%）．
在数列{an}中，若a1=1，an-an-1=n，（n≥2），则该数列的通项an=（　　）
A、
n(n+1)
2
B、
n(n-1)
2
C、
(n+1)(n+2)
2
D、
n(n+1)
2
-1
已知函数f（x）=
2x
2x+1
，
（1）用函数单调性定义证明：f（x）在（-∞，+∞）是增函数；
（2）试求f（x）=
2x
2x+1
在区间[1，2]上的最大值与最小值．
已知函数f（x）=
|lgx|，0＜x≤10
-
1
2
x+6，x＞10
若三个正实数x1，x2，x3互不相等，且满足f（x1）=f（x2）=f（x3），则x1x2x3的取值范围是（　　）
A、（20，24）
B、（10，12）
C、（5，6）
D、（1，10）
在△ABC中，设三边AB，BC，CA的中点分别为E，F，D，则
EC
+
FA
=（　　）
A、
BD
B、
1
2
BD
C、
AC
D、
1
2
AC
奇函数f（x）在[3，6]上是增函数，在区间[3，6]上的最大值为8，最小值为-1，则2f（-6）+f（-3）=
 
．
已知函数f（x）=（x-a）lnx，a∈R．
（Ⅰ）若a=0，对于任意的x∈（0，1），求证：-
1
e
≤f（x）＜0；
（Ⅱ）若函数f（x）在其定义域内不是单调函数，求实数a的取值范围．
已知函数f(x)=
log2x，x＞0
3x，x≤0
，则f[f(
1
4
)]的值是（　　）
A、
1
9
B、9
C、-9
D、-
1
9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网